The Coriolis Force
Fun fact: it’s not a force at all!
Here’s a question to ponder: Say I’m standing on the equator and I shoot a bullet directly north with an extremely powerful gun. Assume that (somehow) my bullet will stay at a constant altitude. Will my bullet:
- straight up and pass directly over the north pole
- upwards, but at an angle such that it will pass to the right of the north pole
- upwards, but at an angle such that it will pass to the left of the north pole
It’s really not obvious. Or at least it wasn’t to me. The Coriolis effect (again, not a force!) explains which of those is the correct answer.
Linear Conveyor Belts
Let’s start with a much simpler question. Imagine there is a series of conveyor belts, like so:
The conveyor belts are moving at different speeds. The bottom one is traveling the fastest while the top one isn’t moving at all. Imagine standing on the bottom one and firing a bullet “directly north”, i.e. directly towards the top of the screen.
Imagine you fire the bullet at the start of the animation when all the red lines are perfectly aligned into a line (restart the animation above to see what I mean). Will the bullet travel:
- straight up and eventually pass directly over the top red line (which isn’t moving)
- upwards, but at an angle such that it will pass to the right of the top red line
- upwards, but at an angle such that it will pass to the left of the top red line
Make a guess and then play the animation below:
The answer is 2. It travels at an angle and passes to the right of the top red line. Why? Even though you fire the bullet “directly north”, the bullet inherits your horizontal velocity as well. The velocity of the bullet is the sum of whatever velocity you have when you fire it plus the velocity the gun adds to the bullet in the direction that you fire it.
Circular Conveyor Belts
Now let’s change the conveyor belts to move in a circle, rather than in a straight line, like so:
Just like in the linear conveyor belts example, we have a series of conveyor belts that are all moving at different speeds. The outermost conveyor belt is moving the fastest and the innermost conveyor belts is moving the slowest.
But notice an important difference between this example and the last one: now the red line segments stay aligned, even as the conveyor belts move at different speeds. Why? Becuase all the belts are moving at the same angular velocity and therefore rotate around the circle the same number of times per second. The outermost belt needs to move faster in order to perform a rotation in the same amount of time as the innermost belt.
Ok now let’s ask the same question as before: Imagine you fire the bullet at the start of the animation when all the red lines are perfectly aligned vertically. Will the bullet travel:
- straight up and eventually pass directly over the center of the circle
- upwards, but at an angle such that it will pass to the right of the center of the circle
- upwards, but at an angle such that it will pass to the left of the center of the circle
Make a guess and then play the animation below:
Again, the answer is 2 - and for exactly the same reason as before. Even though you fire the bullet “directly north”, the bullet inherits your horizontal velocity. This makes the bullet travel “northeast” and pass to the right of the center of the circle.
The Globe
Let’s make one last adjustment. Instead of circular conveyor belts, let’s consider a 2D picture of the globe with the north pole exactly at the center, like so:
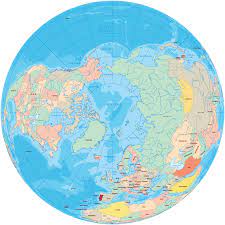
What’s different about this example? In all the previous examples, we were dealing with “flat 2D space”. That means that the trajectory of the bullet looked like a straight line from our “birds-eye” perspective. That’s no longer true. We’ve now projected the top of a sphere (the northern hemisphere of the globe) onto a 2D circle by flattening it out. Distances on our projection don’t faithfully correspond to distances on the sphere. In particular, since the outer edges of the sphere (near the equator) have been flattened more than the center of the circle, the bullet appears to move slower at the edges of the circle. This effect can be seen by the non-uniform spacing of the concentric circles. The true distance between consecutive circles is constant, but it doesn’t appear that way in our projection.
Importantly, though, one fact stays the same. The outermost regions of the circle (and sphere) are still moving faster than the innermost regions - exactly as they did when we were dealing with circular conveyor belts.
You guessed it; let’s ask the same question as before: Imagine you’re on the equator and you fire a bullet directly north. Will the bullet travel:
- straight up and pass directly over the north pole
- upwards, but at an angle such that it will pass to the right of the north pole
- upwards, but at an angle such that it will pass to the left of the north pole
Make a guess and then play the animation below:
Again, the answer is 2. The bullet travels with a constant northern velocity as well as a constant eastward velocity (which it picked up from you as the source). This, combined with the spherical geometry of the globe, makes the bullet’s path look like a spiral that veers to the right of the north pole. Unlike in the circular converyor belt example, eventually the bullet does pass directly over the north pole. The simulation assumes it always travels north with a fixed velocity, and the north pole is the northernmost point, so it has to hit it eventually.
The Observer and “Fictitious Forces”
Every animation so far has take the perspective of a birds-eye observer stationed high above the north pole. What if we instead visualized the globe example, but took the perspective of the observer who is firing the bullet. The important difference is that, according to the observer, they are not spinning in a circle around the globe. They are stationary.
What might that look like?
From the reference frame of the (rotating) observer, it looks like the bullet starts traveling directly north but then oddly accelerates to the east. When viewed from the perspective of observer, this eastward acceleration is hard to explain. However, having come to this through a series of much more straightfoward examples, we now know that this eastward motion is just a consequence of the eastward velocity the bullet picked up from the observer who fired it (who we assumed was standing on the equator). There is no actual acceleration.
This sort of “unexplained motion” has a funny name - it’s called a “fictitious force”. It’s also called a pseudo-force, an inertial force, and an apparent force. It’s the first time (that I can remember) that I’ve run into this concept. It applies when the motion of an object looks as if there’s some external force acting on it because it’s accelerating (e.g. changing directions in this case), however it’s actually not. The apparent force is coming from the fact that the observer is the one accelerating. In this case, the observer is spinning in a circle, constantly accelerating towards the center of the circle. The bullet is traveling in a straight line (albeit on a curved surface which makes it hard to see).
The Coriolis Effect
This finally brings us to the coriolis effect. We’ve actually already fully explained it, but to summarize:
The Coriolis effect describes the tendency for things (usually winds) to accelerate to the east when traveling north and to accelerate to the west when traveling south.
Or wait… actually that’s not quite right. That’s only true in the northern hemisphere. What’s different about the southern hemisphere? Let’s take a look:

The only difference is that when you view the globe from the south, it spins in the opposite direction. Working through all our examples while changing the direction of rotation will make it clear that in the southern hemisphere, the Coriolis effect is reversed, i.e.:
In the southern hemisphere, winds have a tendency to accelerate to the east when traveling south and accelerate to the west when traveling north.
Hurricanes
The canonical example of the Coriolis effect is that hurricane winds create a spiral in one direction in the northern hemisphere and the opposite direction of the southern hemisphere.
To understand this, you first have to know that the center of a hurricane is an area of low pressure. Winds generally want to move towards low pressure areas and so winds pulled towards the center of the hurricane from all directions.
How can we visualize this? Actually, we already have. In the globe examples above, we were treating the north pole as a the destination of the bullet. Instead, let’s imagine the north pole is the center of the hurricane and the object traveling towards it is air. If we assume that the air travels at a constant northern velocity (probably a bad assumption), our previous animations are exactly what we’re looking for:
