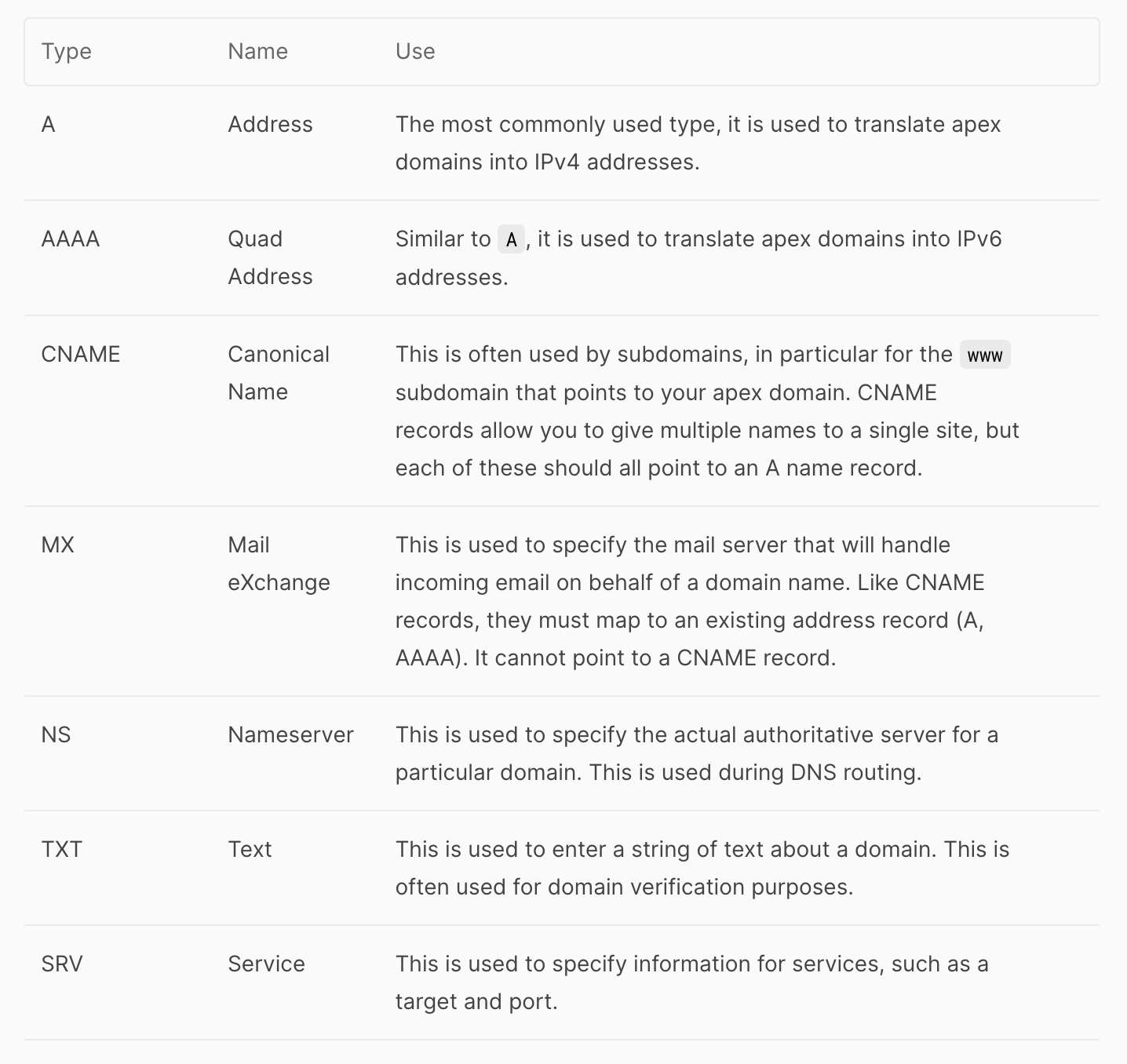
In this post we’re going to build an operator together. Actually, not just one operator, but a whole family of operators.
What do I mean by “an operator”? I mean something like \(+\), \(\cdot\), or \(-\). Also, all the operators we’re going to build are “binary” operators meaning they take 2 numbers as inputs and produce 1 number as an output (again, like plus, minus, etc). Actually the first one doesn’t really need to be a binary operator, but we’re going to make it one just for consistency.
Oh, and one more thing before we begin. This, like any math exposition, will be much more interesting if you take an active role. Don’t just read this from top to bottom. Pause and try to predict the next step for yourself. Work out the examples for yourself before looking at my solutions.
𝙾1
Ok let’s get started! Here’s our first “binary” operator:

In case this is confusing, let me explain.
The symbol I’m using for my operator is a big 𝙾. Why that one? I dunno, why is plus a cross? Why is multiplication sometimes a star and sometimes a dot (and sometimes just omitted)? I just wanted to pick a symbol that wasn’t already used and I picked a big 𝙾.
Ok, so our operator takes 2 numbers, which I’ve denoted as \(a\) and \(n\) and just returns \(n+1\). Yes, it completely ignores the first number and does nothing with it. That’s why I said before that this first operator is kinda of a fake “binary” operator (it’s really a unary operator that only needs 1 number as input).
Sanity check: let’s make sure you understand this operator. Can you solve these exercises?


𝙾2
What’s next? Well, we’re going to define our next operator in terms of the last one (and itself).

This one is more confusing, so bear with me.
The symbol I’m using for this operator is two big 𝙾s. This one really is a binary operator and takes two numbers as inputs which (again) I’ve denoted as \(a\) and \(n\).
If \(n = 0\), this operator returns \(a\). If \(n > 0\), then this operator is defined recursively in terms of itself and the operator we started with (the one with just one 𝙾).
I suspect working through an example will be much more helpful for this one.


Did you get it? If not, that’s totally OK – I grant that it probably wasn’t super obvious what I was going for yet – but from now on I think it’s extra important to work through the examples yourself first.
I went through that example in meticulous detail, step by step, but all those brackets make things pretty hard to read so, if you don’t mind, I’m going to write things without them in the future – like this:

Just remember that when you evaluate, you always evaluate from right to left.
Now that hopefully you know what I’m asking, here are two more examples for you to work out on your own:


Now that you have a couple examples under your belt, do you have a guess at what this operator is, in disguise?

(it’s plus!)
𝙾3
Let’s move to the next one. The definition for the next operator looks almost identical to the last:

I’m hoping you’re getting the hang of things by now so I’m going to write less words and jump right to the exercises:


At this point (just like last time), it’s useful to try to guess what this operator is in disguise. Try more examples if you have to.
Here’s my take:

(it’s multiplication!)
𝙾4
Before we even begin, can you guess how we will define the next operator? I bet you can get pretty close, although I suspect you might get the \(a𝙾𝙾𝙾0\) wrong.

And before even working out any examples, can you guess what this operator will be in disguise?
Either way, here’s your exercise:


Recap
Let’s take a second and realize what we’ve done. We’ve defined addition in terms of +1 (the successor operator). We’ve then defined multiplication in terms of addition. And lastly we’ve defined exponentiation in terms of multiplication. It’s not groundbreaking, but it’s pretty cool!
Here’s a recap in picture form:

𝙾n… and beyond?
At this point, I think the “real math” can start! It’s time for me to stop telling you exactly what to do and time for you to start exploring. But in case it’s helpful, here are some questions that come to mind – at least for me. And I’ll probably explore some of them in future posts.
- The most obvious question: What’s next?? Can you guess it before you work it out? And what’s after that?
- Notice that we’ve defined addition, multiplication, and exponentiation – but only when \(n\) is a non-negative integer. But you already know how to extend those to rational (and real) numbers. Can you extend whatever comes next as well?
- Why are all the cases where \(n = 0\) different (\(a𝙾0 = 1\), \(a𝙾𝙾0 = a\), \(a𝙾𝙾𝙾0 = 0\), \(a𝙾𝙾𝙾𝙾0 = 1\), etc.)? Doesn’t that seem kind of gross? Shouldn’t our operators have more symmetry in their definitions? What if we decided to change the definitions to make them more similar?
- We’ve defined these operators in a very “natural numbers” sort of way. The number of 𝙾s is either 1, 2, 3, 4, etc. Could we… extend this to the reals? What would the operator with 1.5 𝙾s be?
- \(log\) is a (unary) function that kind of turns multiplication into addition. More precisely, it has the property \(log(a \cdot b) = log(a) + log(b)\). Less precisely, it kind of “removes a 𝙾”. Can we find a function that turns exponentiation into multiplication? Or an arbitrary number of 𝙾s to one less than that?
Have fun!
References
Unsurprisingly, the idea of building up operators recursively is not my idea. These are called Hyperoperations. Apparently, this formulation was first written down by Reuben Goodstein and you’ll find a version of it at the bottom of page 7.
If you want to turn this idea into a puzzle for your friends, you can use Goodstein’s function (written in python) and just ask them to explain what this function does:
def g(k, a, n):
if k == 1:
return n + 1
elif k == 2 and n == 0:
return a
elif k == 3 and n == 0:
return 0
elif n == 0:
return 1
else:
return g(k-1, a, g(k, a, n - 1))