Polynomials are just numbers in base x

Here’s a neat idea: A polynomial is just a number in (an unknown) base $x$.

Bases

When we use the number $427$, what do we mean? Normally, we implicitly work in base-10, but since we’ll be exploring other bases in this post, let’s be explicit and use the notation ${427}_{10}$.

So what does ${427}_{10}$ mean? It’s shorthand for:

$$4({10}^2)+2({10}^1)+7({10}^0)={427}_{10}$$

What about if we change the base from base-10 (decimal) to base-2 (binary)? What does ${427}_2$ mean?

$$4(2^2)+2(2^1)+7(2^0)={427}_2$$

More generally, what does ${427}_x$ (427 in base-x) mean?

$$4x^2+2x^1+7x^0={427}_x$$

In this way, we can use a number to represent a polynomial expression in much the same way that we already use numbers to represent arithmetic expressions.

But… 427 is not a binary number!

Some careful readers may have objected at the thought of ${427}_2$ being a base-2 number. After all, binary numbers are comprised of zeros and ones, and nothing else.

This is normally true. Normally, we do not allow a single digit to be equal to or larger than the base. For base-10, this means no digits larger than 9. For base-2, this means no digits larger than 1. However, let us suspend our normal conventions for a moment. Is there really anything wrong with using a digit that is larger than the base?

$4(2^2)+2(2^1)+7(2^0)$ is a perfectly reasonable expression, even if it is not the conventional way we express numbers in base-2. As my three year old loves to remind me, if you add one to $29$, there’s nothing wrong with “twenty-ten”.

So, although we may be on somewhat unfamiliar ground, let’s continue exploring a world in which we allow digits to be arbitrarily large and see where this takes us.

Addition

First, we re-learn addition, without carryover. Consider the example of adding ${47}_{10}$ and ${94}_{10}$. Here is what we’re used to:

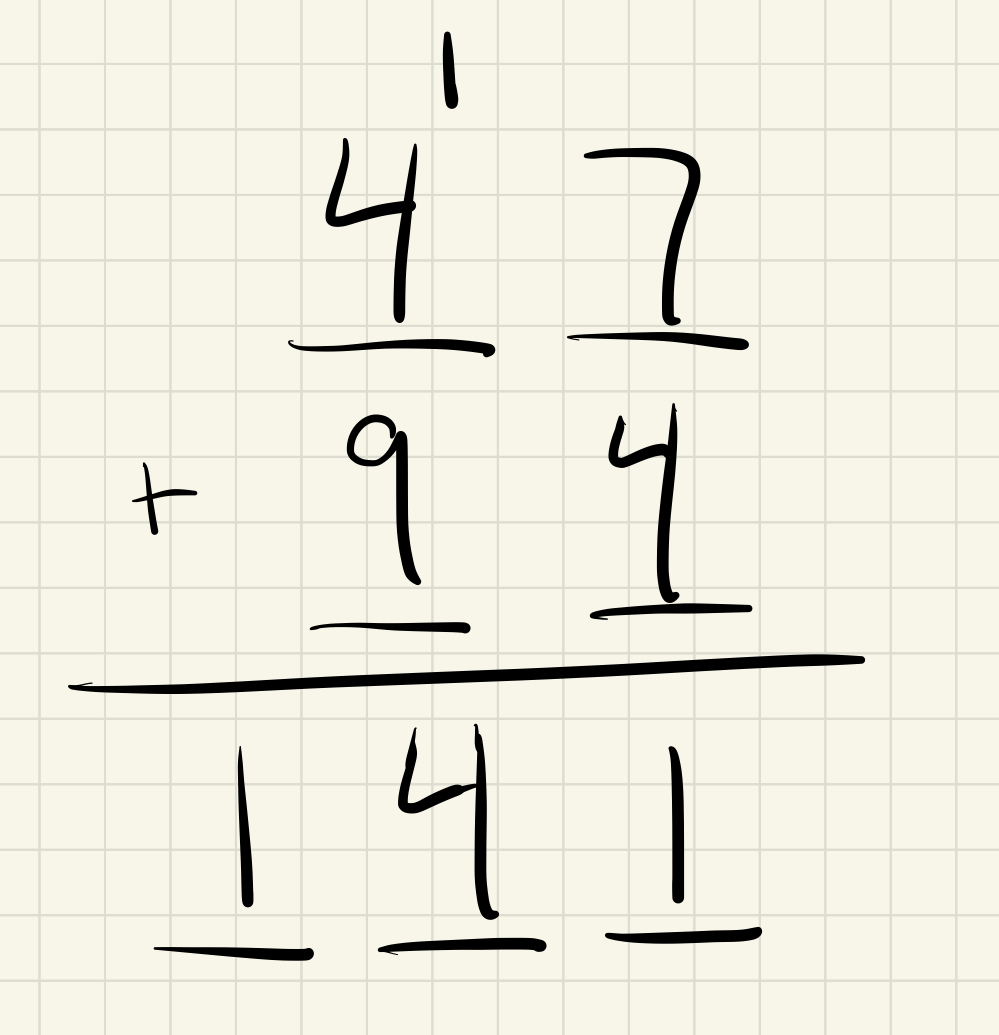
Notice two things. First, when we add 7 and 4, instead of writing 11 down, we only write a 1 and we carry the 1. Second, our answer is the number ${141}_{10}$, which is equivalent to the expression $1({10}^2)+4({10}^1)+1({10}^0)$.

If we now try this addition again, but we allow digits of arbitrary size and forget the carryover rule, it would look something like

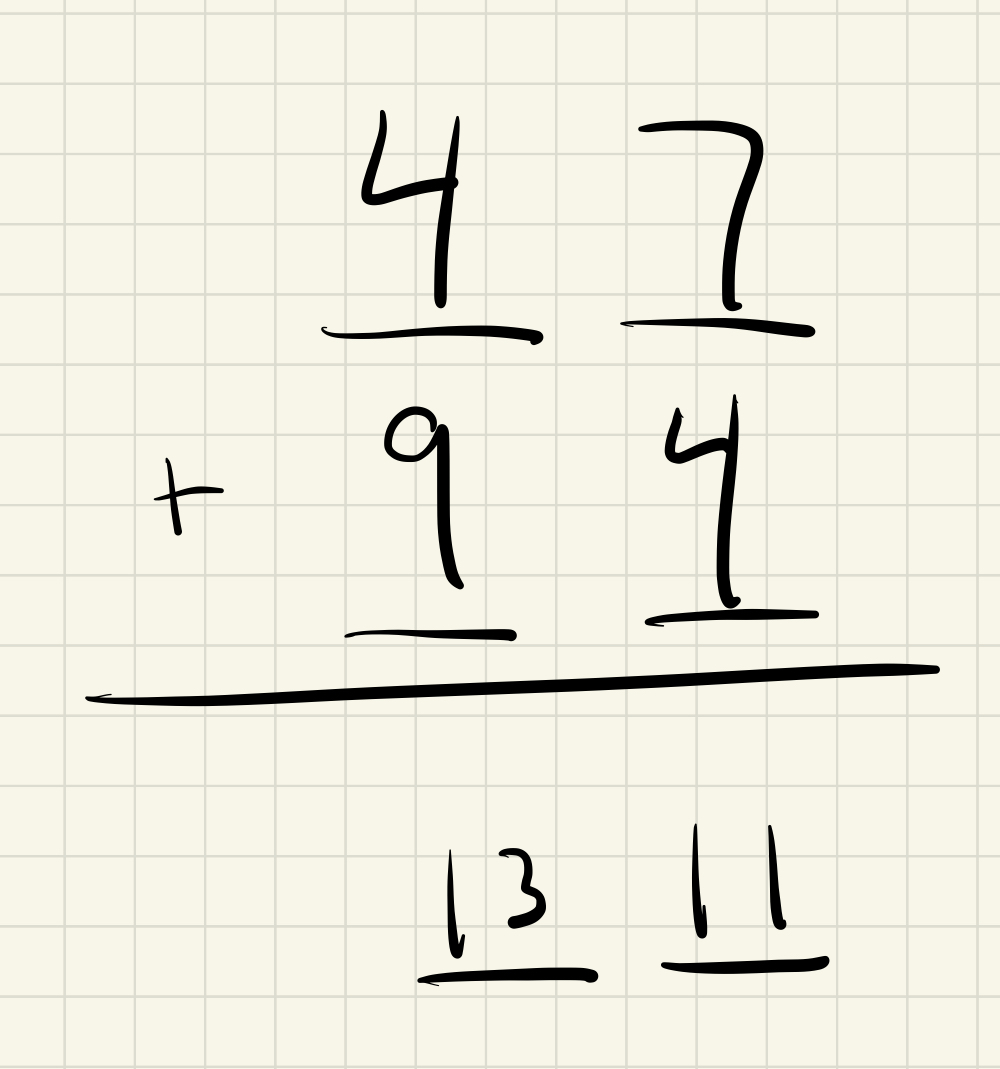
This answer is hard to write down in standard form; ${1311}_{10}$ looks wrong since it’s unclear where one digit ends and the next one starts. To solve this, let’s make up a new convention where we wrap each digit in brackets, like so: $[13][11{]}_{10}$. Also, we can sidestep this problem completely and write our answer as an expression: $13({10}^1)+11({10}^0)$. Notice that this expression is equal to our previous answer of $1({10}^2)+4({10}^1)+1({10}^0)$.

Adding polynomials

If the example above felt pointless, then hopefully this will help. What is $4x+7$ plus $9x+4$? Is it:

• a) $1x^2+4x+1$ (aka ${141}_x$) or
• b) $13x+11$ (aka $[13][11{]}_x$)

It’s clearly b, but why? Why does carrying over make intuitive sense when we’re dealing with numbers in base-10, but not when we’re dealing with polynomials?

At the risk of being overly pedantic¹, in base-10, we can convert a 10 in one place into a 1 in the next place because $10({10}^n)=1({10}^{n+1})$. For base-2, we can convert a 2 in one place to a 1 in the next place becuase $2(2^n)=1(2^{n+1})$.

When we’re dealing with polynomials in base-x, we can’t carry over because we don’t know how many $x$’s you need to make one $x^2$. So we don’t, and everything works out fine - just as it did in our base-10 addition example when we added ${47}_{10}$ and ${94}_{10}$ to get $[13][11{]}_{10}$. To really drive the analogy home, here’s the same picture from but now with $x$’s:

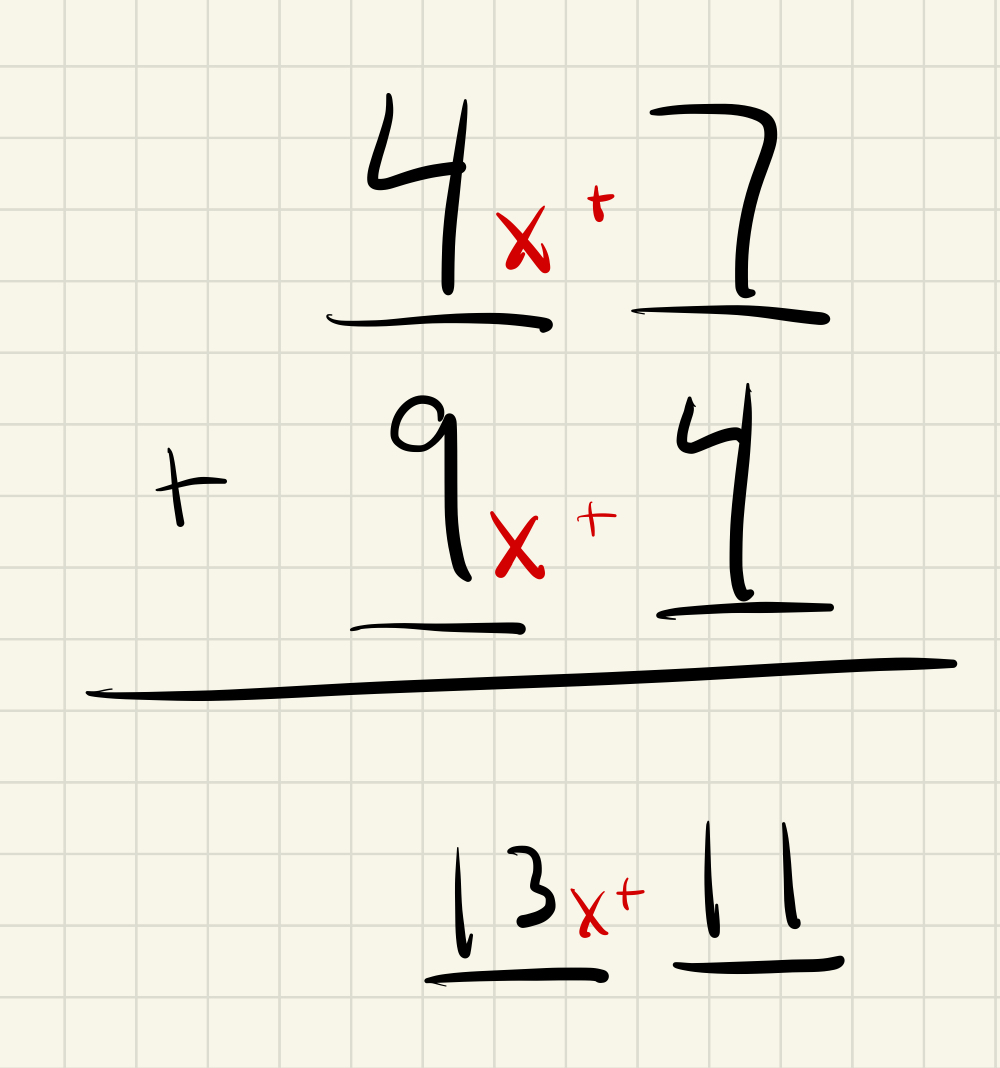
Neat. But… is it useful?

By treating polynomials as numbers (but in some unknown base $x$) certain operations become “obvious”, or at least obvious after you un-learn carryover.

We just saw how adding the polynomials $4x+7$ and $9x+4$ was as easy as adding the numbers ${47}_{10}$ and ${94}_{10}$. But that’s not very compelling since adding polynomials is easy to begin with.

How about multiplying polynomials? What if instead of adding $4x+7$ and $9x+4$, we multiplied them? In school you probably learned how to multiply polynomials with the FOIL mnemonic. But if you just treat polynomials as numbers, then you already know how to multiply them:

By treating polynomials as numbers, we can use the standard method for multiplying numbers to multiply polynomials. I think that’s quite a bit more compelling, but we can do even better.

What is $6x^2+21x-7$ divided by $3x-1$? Again, we treat polynomials as numbers and use our standard method for long division:

Going farther

Solving polynomial equations

This framing gives us a new way to think about solving polynomial equations. When solving an equation for $x$, you are finding the base which makes both sides of the equation equal. Consider an example we’ve already used above, what is the $x$ that solves this equation?

$$1x^2+4x+1={141}_{10}$$

It’s quite easy to see that, in this case, $x=10$ solves the equation. What about this one?

$$1x^2+4x+1={13}_{10}={141}_2$$

Again, it’s obvious that $x=2$ solves the equation since ${141}_2$ is just shorthand for $1(2^2)+4(2)+1$. The solution won’t always be this obvious, of course, but in principle it’s the same idea.

Negative and non-integer bases

We know that when solving an equation for $x$, the answer is not always a positive integer. And we just showed above that solving an equation for $x$ is equivalent to finding the appropriate base. This implies that bases do not always need to be positive or integers. Take this equation, for example:

$$4x^2+2x+7=-13$$

Solving the equation results in $x=-\frac{3}{2}$. Using our idea of treating polynomials as numbers, we can reformulate this equation like so:

$${427}_{-\frac{3}{2}}=-{13}_{10}$$

Nothing revolutionary, but an interesting perspective.

Prime polynomials?

Now that we’re treating polynomials as numbers, let’s try to extend a property normally reserved for numbers: the property of being “prime”. We define a prime number to be one that is not a product of two smaller numbers. ${14}_{10}$ is not prime, since it’s the produce of $7_{10}$ and $2_{10}$. But what about in base-x?

$${14}_x=x+4$$

Try to find two smaller numbers (in base-x, i.e. polynomials) that can multiply to ${14}_x$. I certainly can’t.

I’ve only just thought of this idea (primeness for polynomials), and so I haven’t yet thought of any useful applications for it, but math has a long history of finding useful applications for bizarre and esoteric ideas.

1. We may have crossed that bridge long ago. ↩