Chess evaluations are weird
In the last post, I dealt a lot with chess evaluations. In doing so, I was forced to arbitrarily give a numeric value to a position where one player had forced mate. This got me thinking….
Why did it seem arbitrary to give a numerical value to a position with forced mate? After all, isn’t every position either a forced mate, a forced draw, or a forced loss? If this isn’t clear to you, consider this: chess is just a much more complicated version of tic-tac-toe. Both games are deterministic and have no hidden information. This means that, with infinite computing power, one could compute every possible game that could result from a given position. This also means that one could compute whether or not there is a sequence of moves that forces a win from the given position.
This is blatantly obvious to any elementary schooler in the case of tic-tac-toe, but is less obvious for chess. However, despite the practically infinite difference in the amount of computing power needed for these two games, they are in principle equally simple to play: find a move that guarantees a win, if no such move exists then find a move that guarantees a draw, otherwise you lose.
So, with that context in mind, isn’t an evaluation that returns anything other than “forced mate”, “forced draw”, or “forced loss” the weird and arbitrary thing? Why can two positions that are both forced draws get different evaluations? The practical answer is obvious: because we do not have infinite computing power and therefore we don’t know that these two positions are forced draws (and if we did, the evaluation would be +0). However, let me play devil’s advocate…
While everything I said above is - I think - objectively true, there does still seem to be room differentiate between two positions that both have the same theoretical outcome (e.g. forced draw). Let’s consider tic-tac-toe, since it’s so much easier to wrap our heads around. As you probably know, tic-tac-toe is a forced draw for every starting move that X can make. But I claim that the top center square is still a “bad” starting move for X. Why? Because there is no following move that O can make such that X can guarantee a win. Put another way, if you play in the top center as X, you’ve made O’s life extremely easy; they can’t possibly make a losing move. Contrast that with the starting in the top right square. In that case, all moves except one (the center) are losing for O. Here’s a picture:
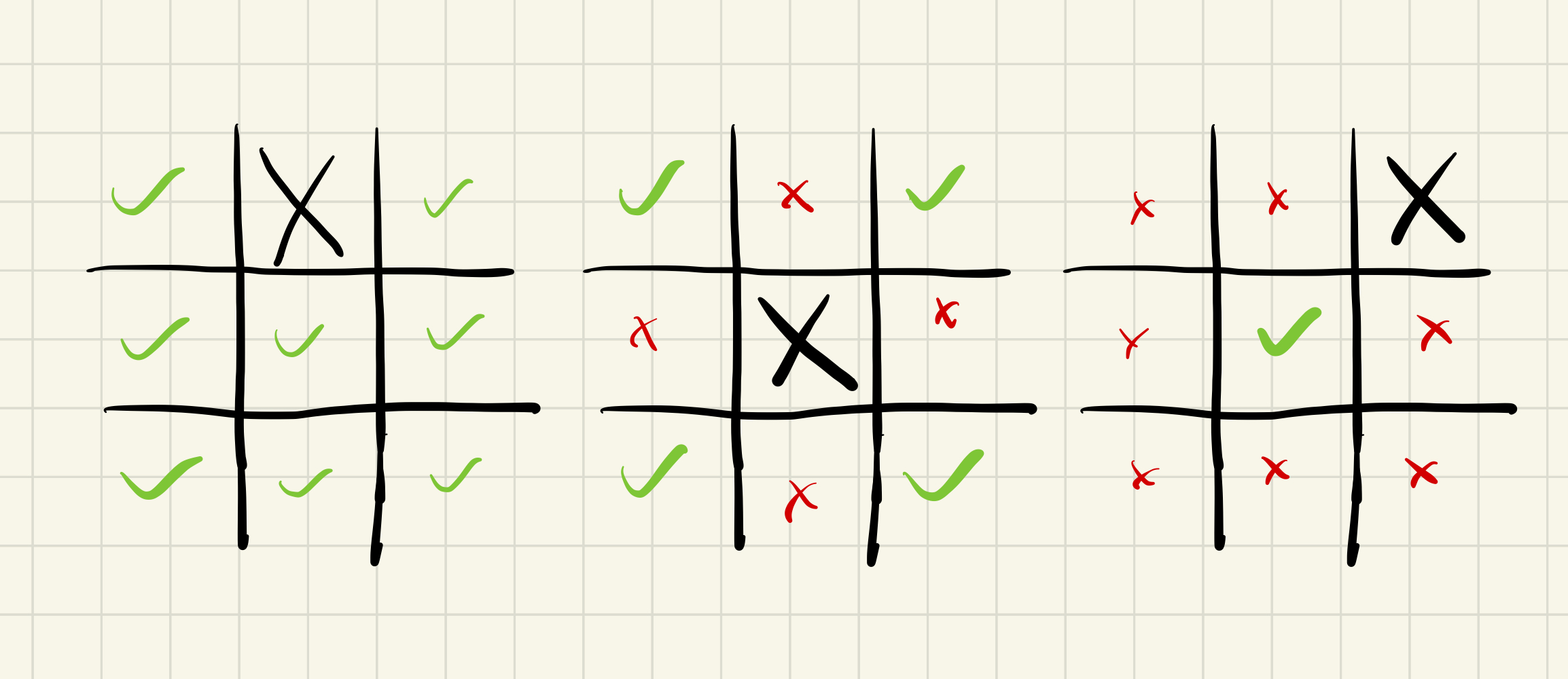
Losing squares for O are marked with a red x while drawing squares are marked with a green check mark, for three different starting positions for X.
To be clear, if O plays perfectly, they can force a draw for any starting X position - including the top right - but they might not play perfectly. I think that’s the crucial point. Two positions may have the same outcome with perfect play, but it may be much harder to play one position perfectly vs. another. In those cases, given our inability to play most games perfectly, then it might make sense to give different evaluations to those positions.
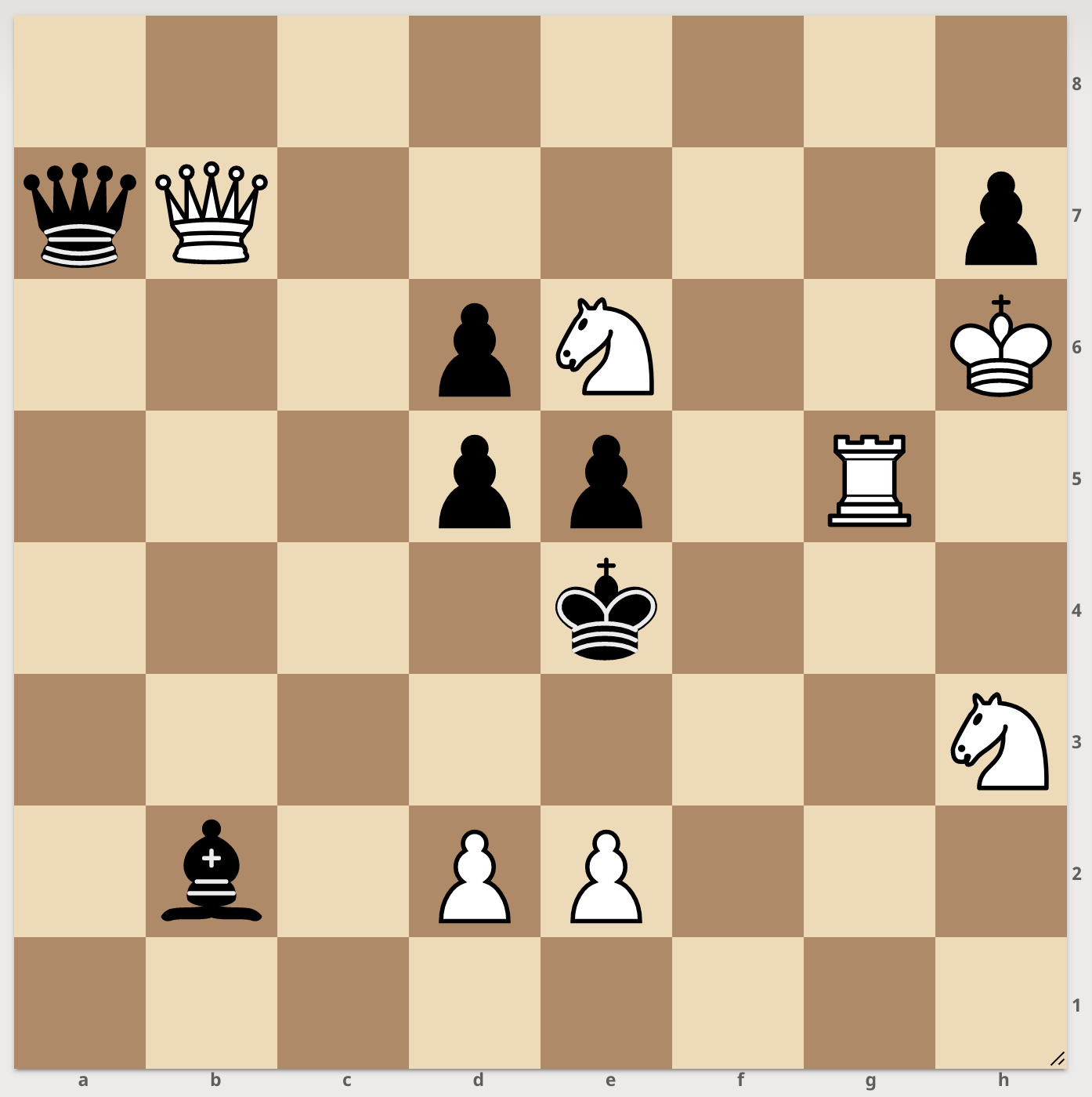
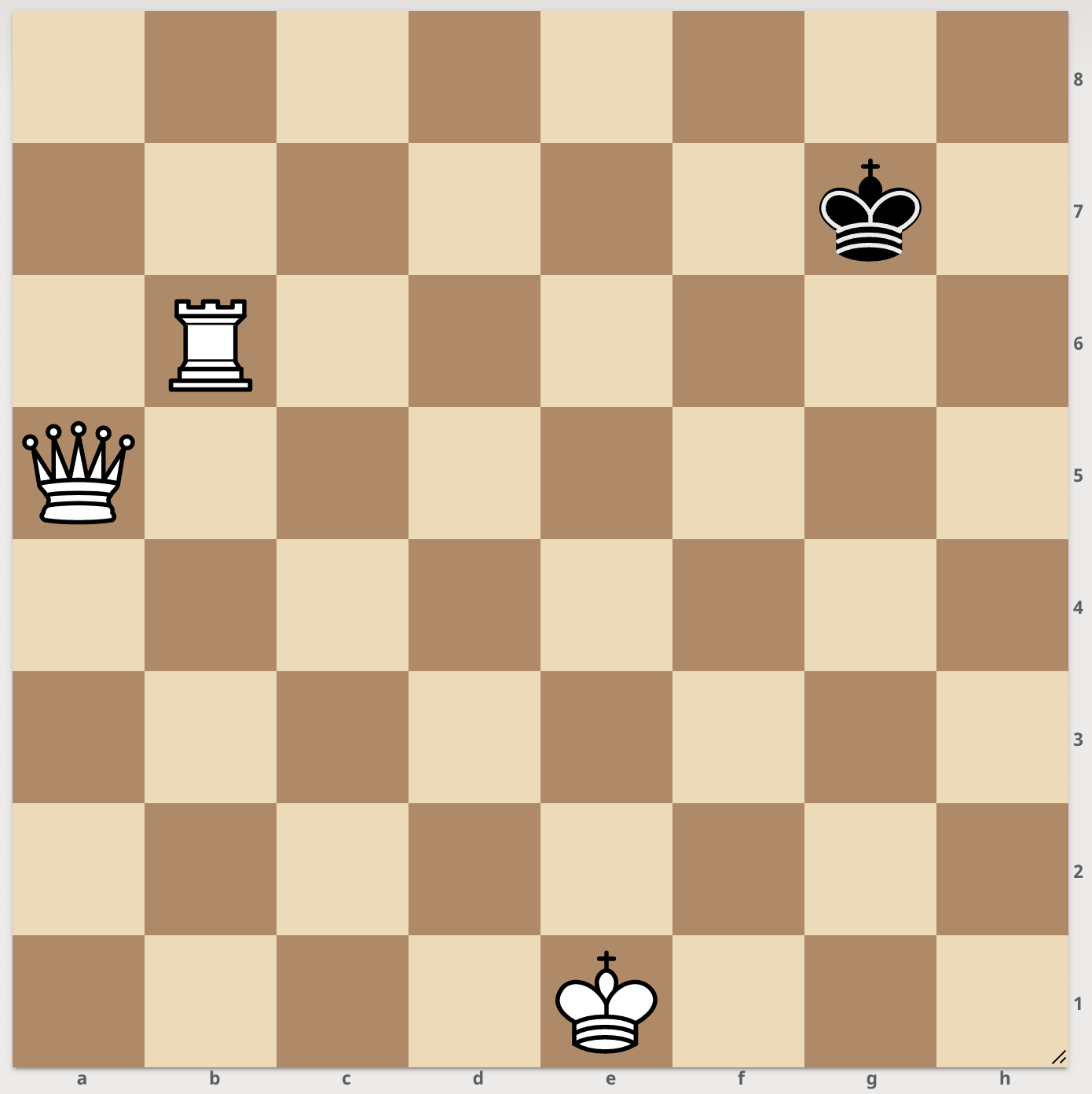
To close this out, consider the following two chess positions, both of which are forced mate in two for white. To a computer, these would be trivially the same, but to a human? You be the judge.