Winning in chess
When is a chess game winning?
Chess commentators use the term winning like mathematicians use the term trivial - incorrectly. They’ll see a position with even material, but black has doubled pawns, and say that white is winning. Well, not at my level… So, I set out to see for myself when a position is really winning.
Before we answer the question, though, let’s make sure we agree on what it means. What do you think white is winning means? If you’re not familiar with the expression, you may interpret it literally: white is winning if white is ahead. In practice, though, it means something closer to: white has an advantage large enough that white can be expected to win. The expression white is better is more analogous to white is ahead.
So what question am I trying to answer? Personal experience suggests that one can have very substantial advantage and yet still manage to not win the game. I’d like to see if this generalizes. More precisely:
I’d like to know the probability that one will win a chess game given a current score of \(x\), for different values of \(x\). Furthermore, I’d like to see how this changes depending on the time control of the game and the Elo ratings of the players involved.
A technical caveat: Chess results are not binary. There’s a third option: a draw. So if we were to literally compute the probability that one wins a chess game, the results would not distinguish between losses and draws. This can result in counterintuitive results. For example, you may think that the higher the Elo rating of a player, the more likely they are to convert a small advantage into a win. However, it’s also true that higher rated players draw more often than lower rated players, which may mean that for small advantages, higher rated players are less likely to win (because they’re more likely to draw). All this is to say that interpreting the probability of winning in the presence of draws is non-trivial, which is why we’re not going to actually compute the probability of winning. Instead, wherever we say “probability of winning”, we will actually compute the “expected number of points”, where losing is worth 0 points, winning is worth 1 point, and draws are worth 0.5 points. This way, we can incorporate draws into our results in a way that does not consider them to be the equal to losses.
There’s one more term you need to be comfortable with in order to understand the analysis below: score. A score refers to the evaluation of the position, often by a strong chess engine. By convention, scores are quoted in terms of pawns, so a score of +1 for white means that white’s position is better by about one pawn. It’s somewhat arbitrary, though, what numerical score you give to a position where one player has forced mate1. For my analysis, I chose +/-25 (as in, ahead or behind by 25 pawns) since that large of an advantage rarely came up without forced mate.
Methods
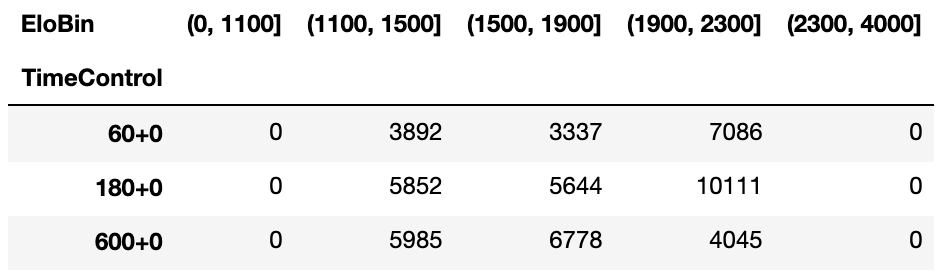
First, I found about fifty thousand games played on Lichess, roughly evenly distributed across a wide range of Elo ratings (1100 - 2300) and three different time controls (60+0, 180+0, and 600+0). Here is the breakdown of number of games in each bucket:
Next, I evaluated each position in each game using stockfish 12, giving it 0.1 seconds of evaluation time per position. If you’re wondering whether stockfish can give a good evaluation with only 0.1 seconds per position, apparently stockfish 10 has a 3200 rating with 0.1 seconds per position2. And stockfish 12 is, well, better.
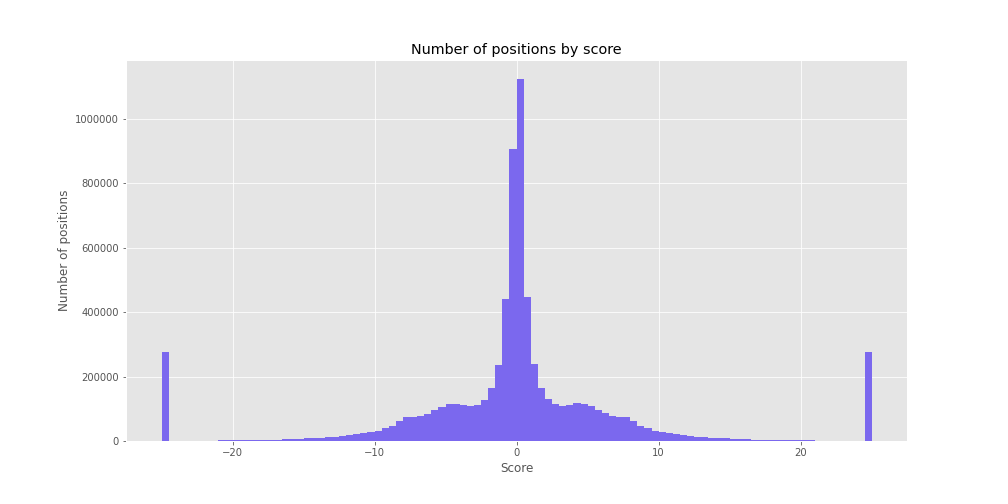
Here is a histogram of stockfish’s evaluations (the scores):
Results
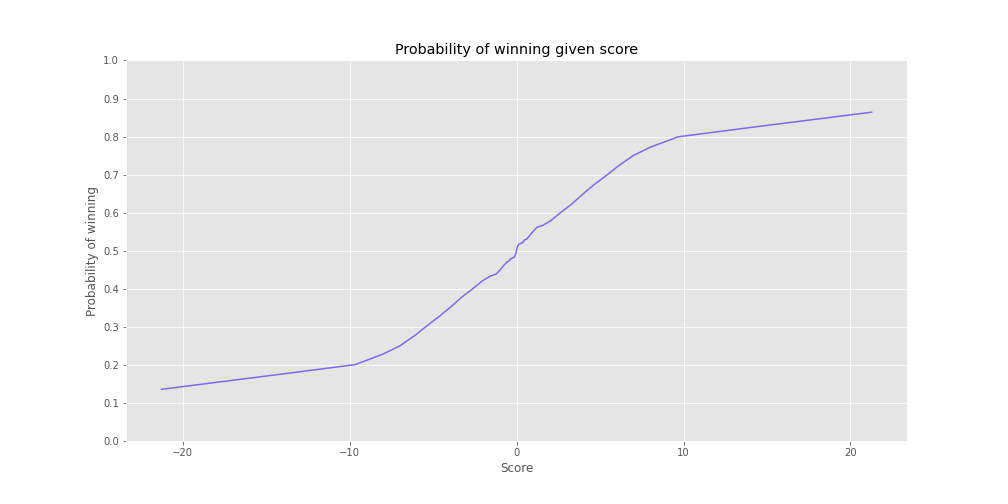
This graph most directly answers the question “what is the probability one will win a chess game given a current score of \(x\)?”. For example, given a current score of 0, your probability of winning is 50%. That makes intuitive sense, since neither player has an advantage.
Given a current advantage of +10, your probability of winning is 80%. +10 is a hefty advantage. You’re up a full queen. I would have expected the probability of winning at that point to be closer to 1. Let’s see how this probability breaks down between the three different time controls.
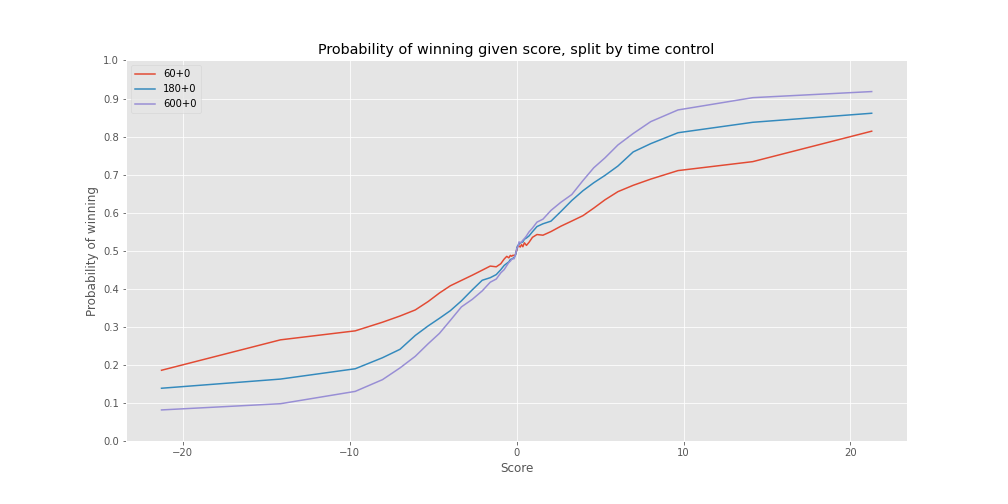
As expected, the longer the time control, the more likely one is to win given an advantage. This makes sense; bullet (60+0) games are wild and chaotic with massive swings back and forth while 10 minute games are, relatively speaking, more measured and predicatable.
If we again look at a +10 advantage, but for 10 minute games this time, we see that the probability of winning increases to almost 90%. I’m surprised it’s not even higher, but this does certainly answer my question: I am not alone in being capable of losing a massive advantage.
How do these probabilities change as we control for the players’ Elos?
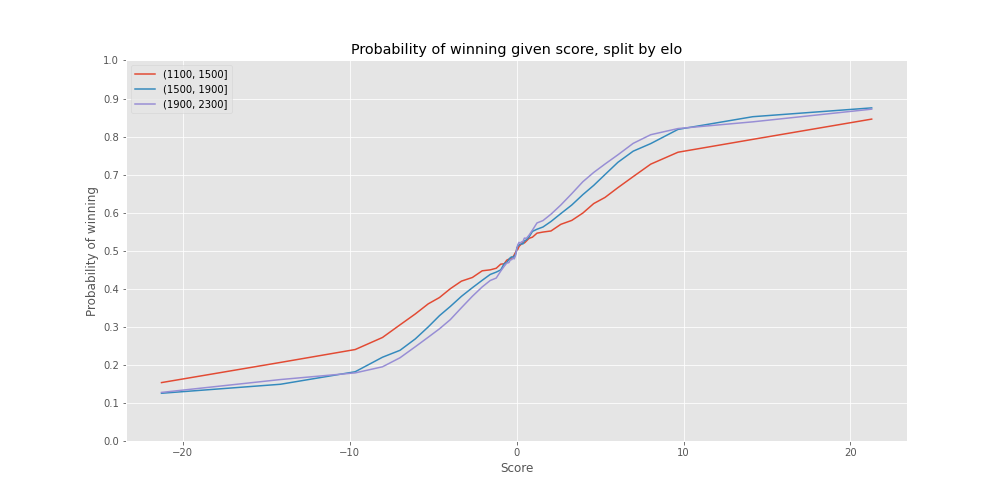
Again, the probabilities vary in the direction that I would expect, but not by as much as I would expect. Higher rated players are more likely to be able to convert an advantage into a win, but they’re not way more likely to be able to do this. Even players in the 1900-2300 range are only about 85% to win a game given a +10 advantage. This is probably the most untuitive finding (and makes me a little skeptical of my analysis).
One thing to note is that these games do include games that end by time forfeit, meaning that one player may be ahead in score but they lost due to thir time running out. That may help explain some of these losses.

This last graph shows the advantage needed in order to have a 65% chance of winning the game. For lower rated (1100-1500) players in the bullet (60+0) time control, you need a massive +14 advantage. For higher rated players in the same time control, you only need an advantage of +5 or +6.
For longer games, the necessary advantage is smaller - dramatically so for lower rated players.
-
The more you think about it, the weirder this becomes. Every position is, after all, one of forced mate, forced mate against, or draw. ↩
-
https://www.chess.com/forum/view/general/i-want-a-good-analysis-with-stockfish-how-long-should-i-do-1-min-1-hour-1-day ↩