Why is the sun stronger at noon?
Everyone knows that the sun is strongest at noon, but why? If you don’t already know, as usual I recommend giving it some thought before you continue. It’s an interesting question and it’s not as obvious as you might think.
A quick bit of terminology before we begin: the solar zenith angle is the angle between the sun’s rays and the vertical. So, by definition, the solar zenith angle is zero when the sun is directly overhead. Ignoring practical considerations like seasons, the earth’s tilt, etc, the solar zenith angle is zero at noon.
Although the complete answer is, I’m sure, much more nuanced than this, I’ve been able to find two main reasons.
- The atmosphere absorbs solar radiation. The amount of atmosphere the sun’s rays pass through varies by time of day, with noon being the least amount of atmosphere and sunrise/sunset being the most.
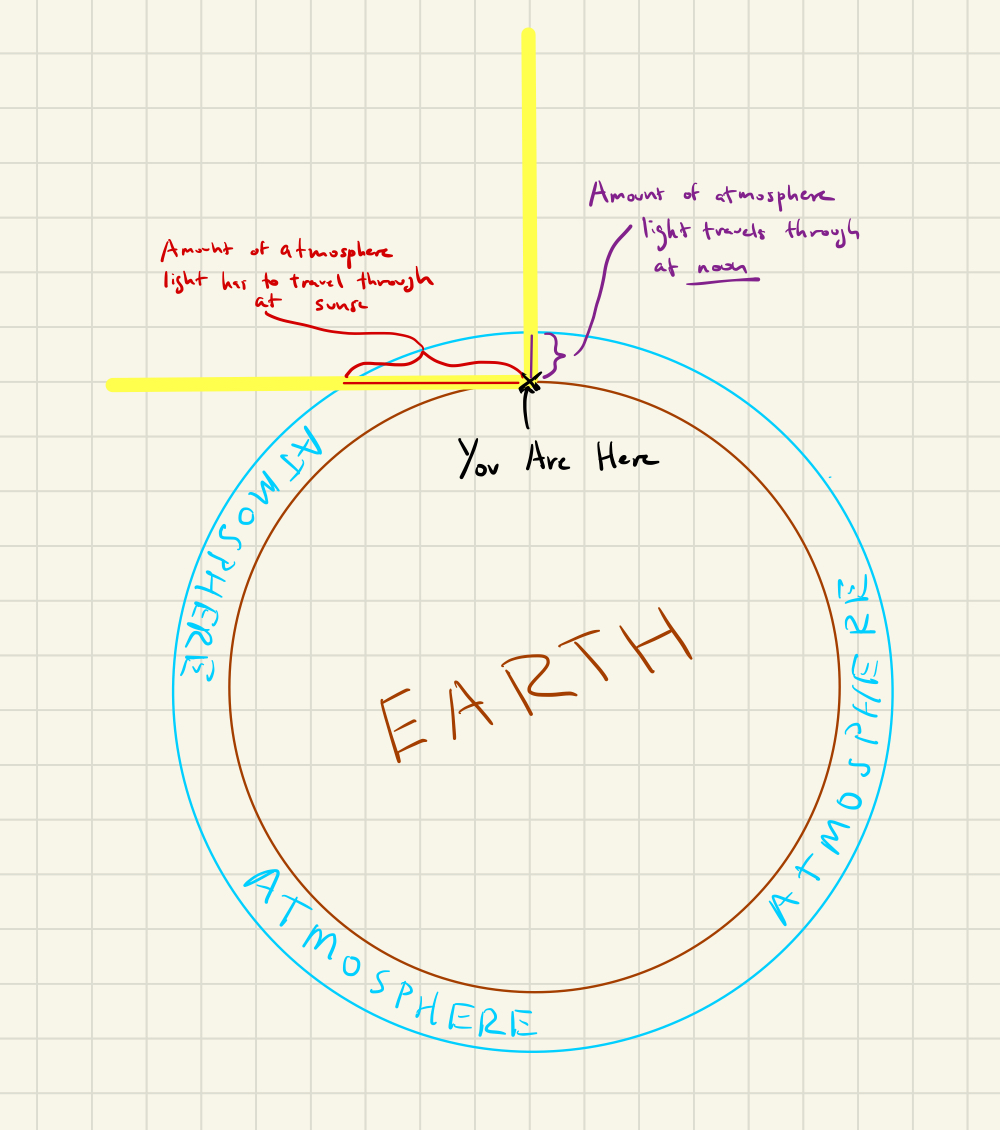
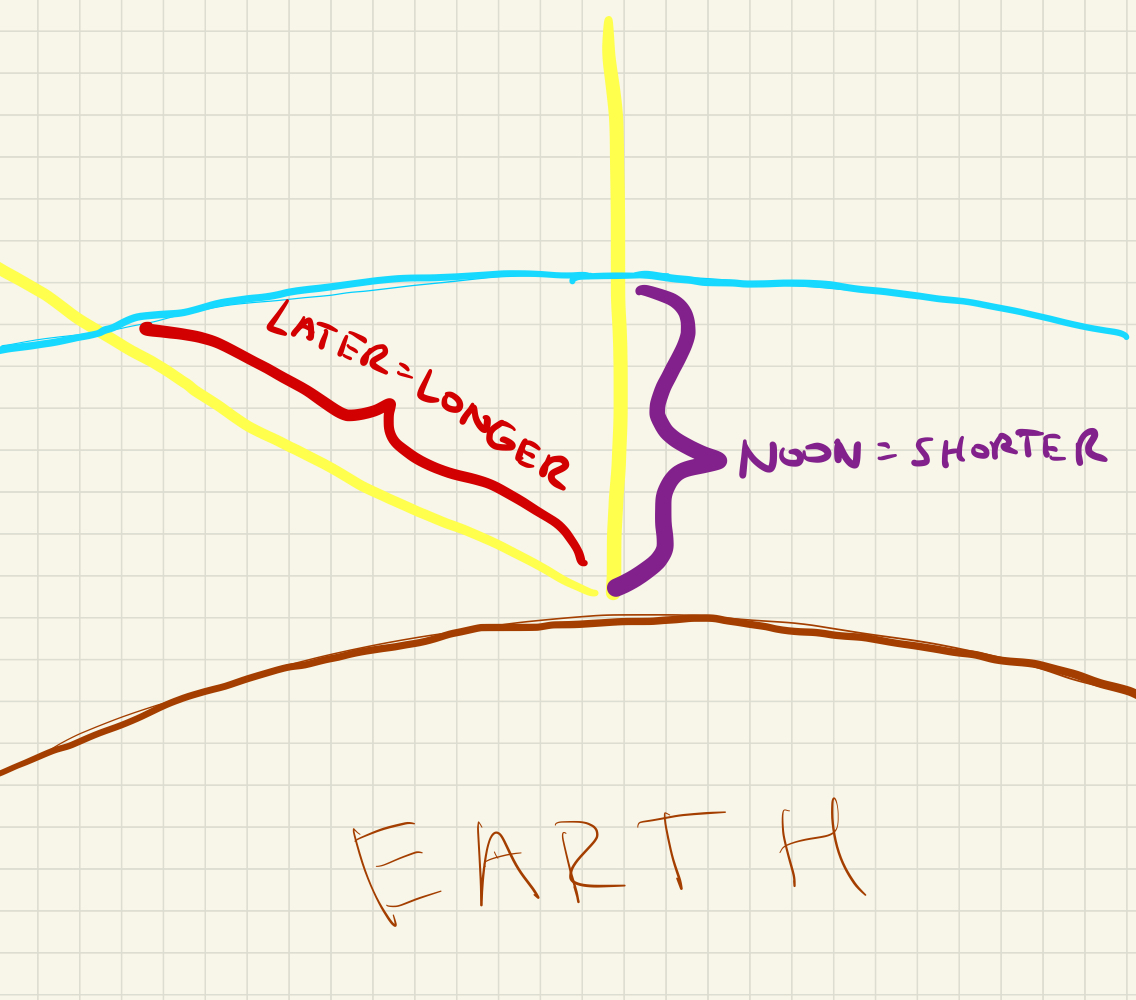
These two graphs show the same thing, one is just zoomed to make it easier to see the differences in the length of atmosphere that light has to pass through at different times of day.
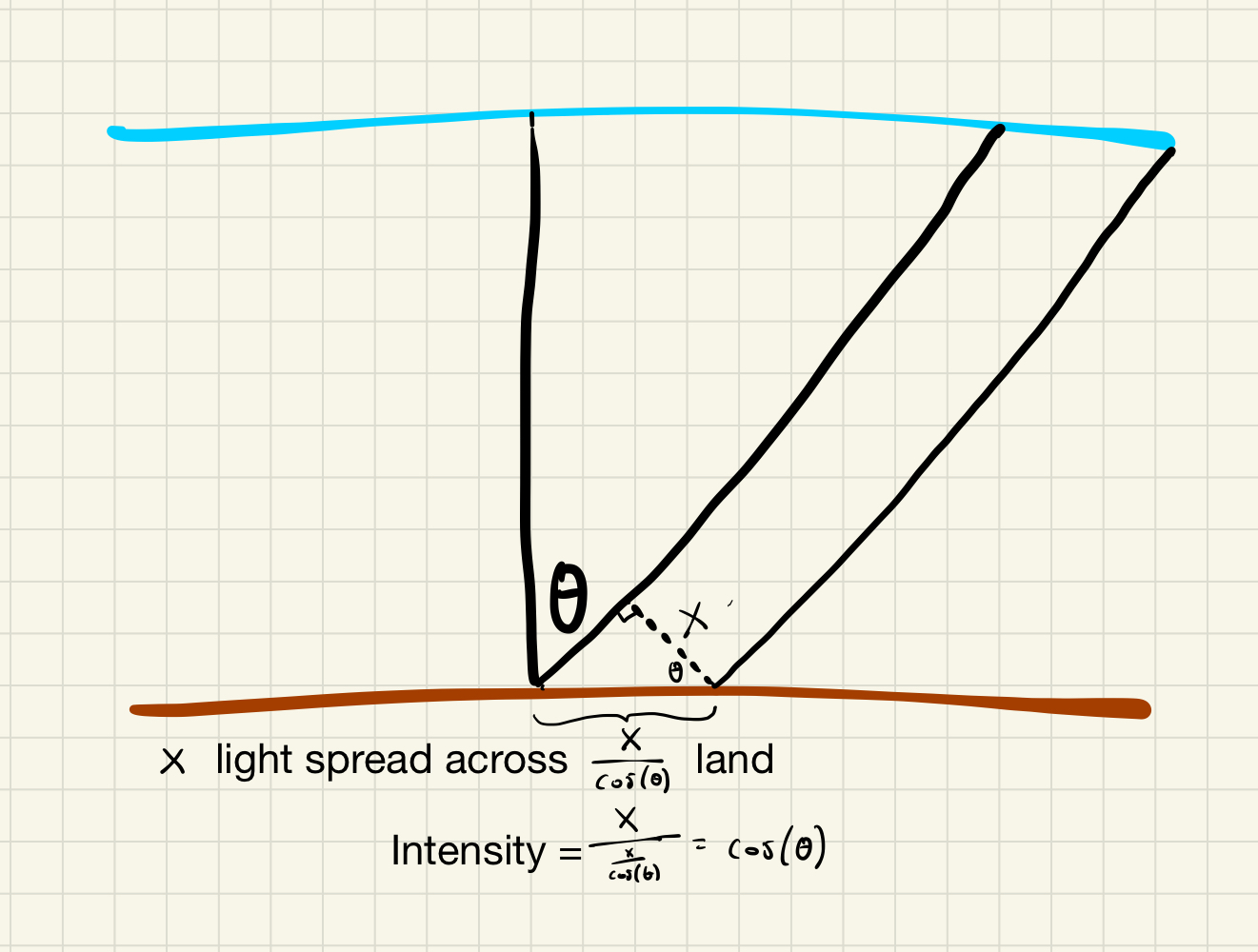
- The angle at which the sun’s rays strike the earth depends on the time of day. At noon, the sun is directly overhead and strikes the ground at a perpendicular angle. For reasons that I will explain later, this results in the largest amount of energy transfer per area of ground.
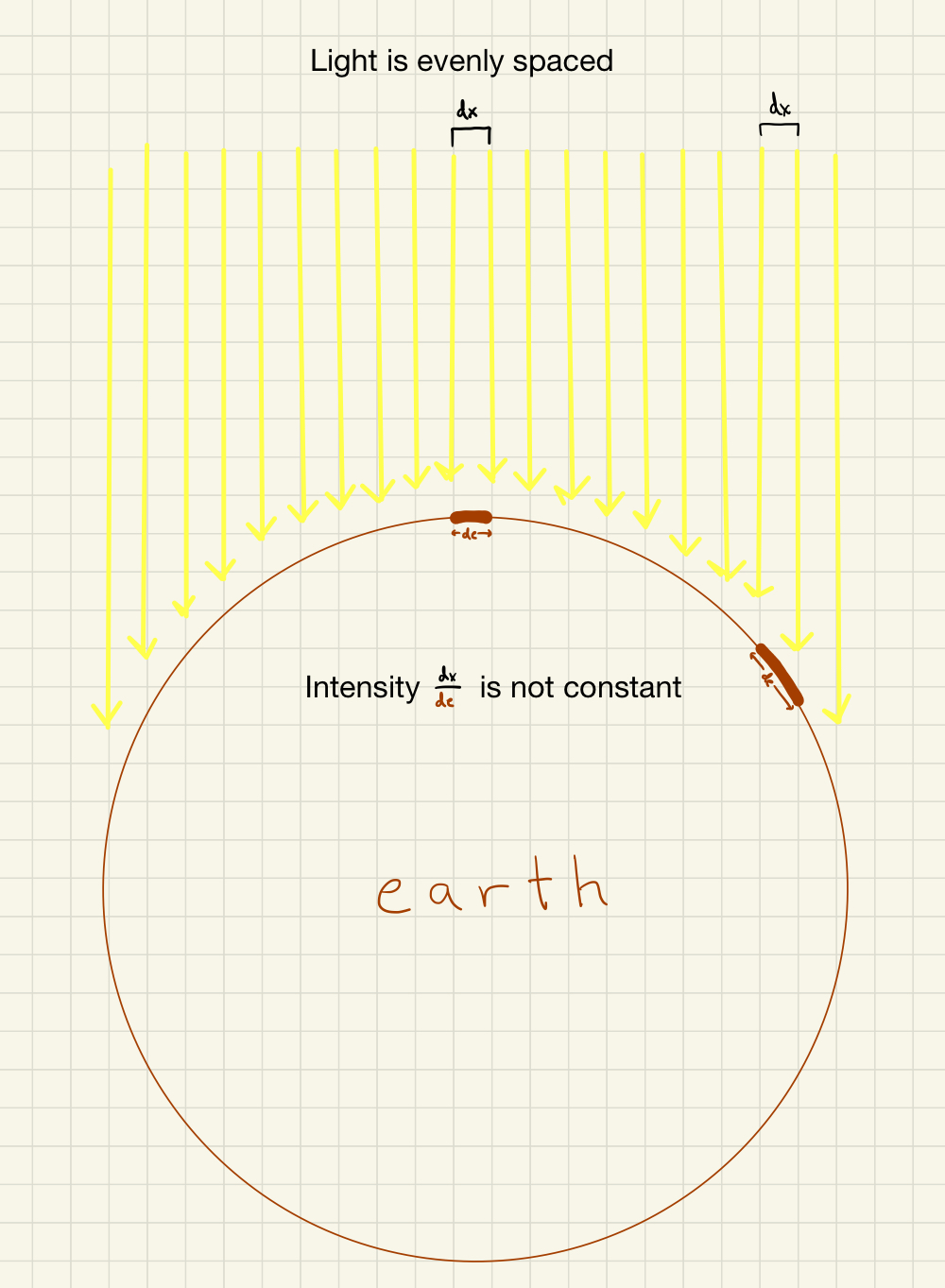
These two pictures demonstrate the same thing in two different ways. The picture on the left shows all points on the earth’s surface at a given instant in time. The picture on the right shows the same point on the earth at two different instances in time. Both are demonstrating that for a constant density of light rays, the larger the solar zenith angle, the more land over which those rays are dispersed, resulting in a lower solar intensity.
It could have been different!
At least with respect to point #1. On the left is a roughly-to-scale picture of the earth surrounded by the atmosphere. The atmosphere is tiny compared to the earth! And that’s the entire reason for this effect. If the atmosphere was very large relative to the earth, like the animation on the right, the distance sun rays travel through the atmosphere (the red line) as a function of time is almost constant. It’s odd to think how different life would be if this minor(?) detail was different.
How much stronger is the sun at noon?
First we need to be more specific about what exactly we’re measuring. How about UV radiation, since that’s has obvious practical implications.
Let’s start with a simple model and see how far that gets us. Suppose that traveling through 1km of atmosphere absorbs 50% of UV radiation, then how much would be left after traving through 2km? After 1km, 50% would be left, and after another km, 25% would be left. More generally, if \(x\)% makes it through each 1km, then \(x^n\)% makes it through \(n\)km.
But what is \(x\)? Nasa says that the ozone filters 97-99% of UV light1. So, for our simple model, we will say that \(3\)% of UV light makes it though “the atmosphere at noon”. We will arbitrarily consider “the atmosphere at noon” to be a distance of 1.
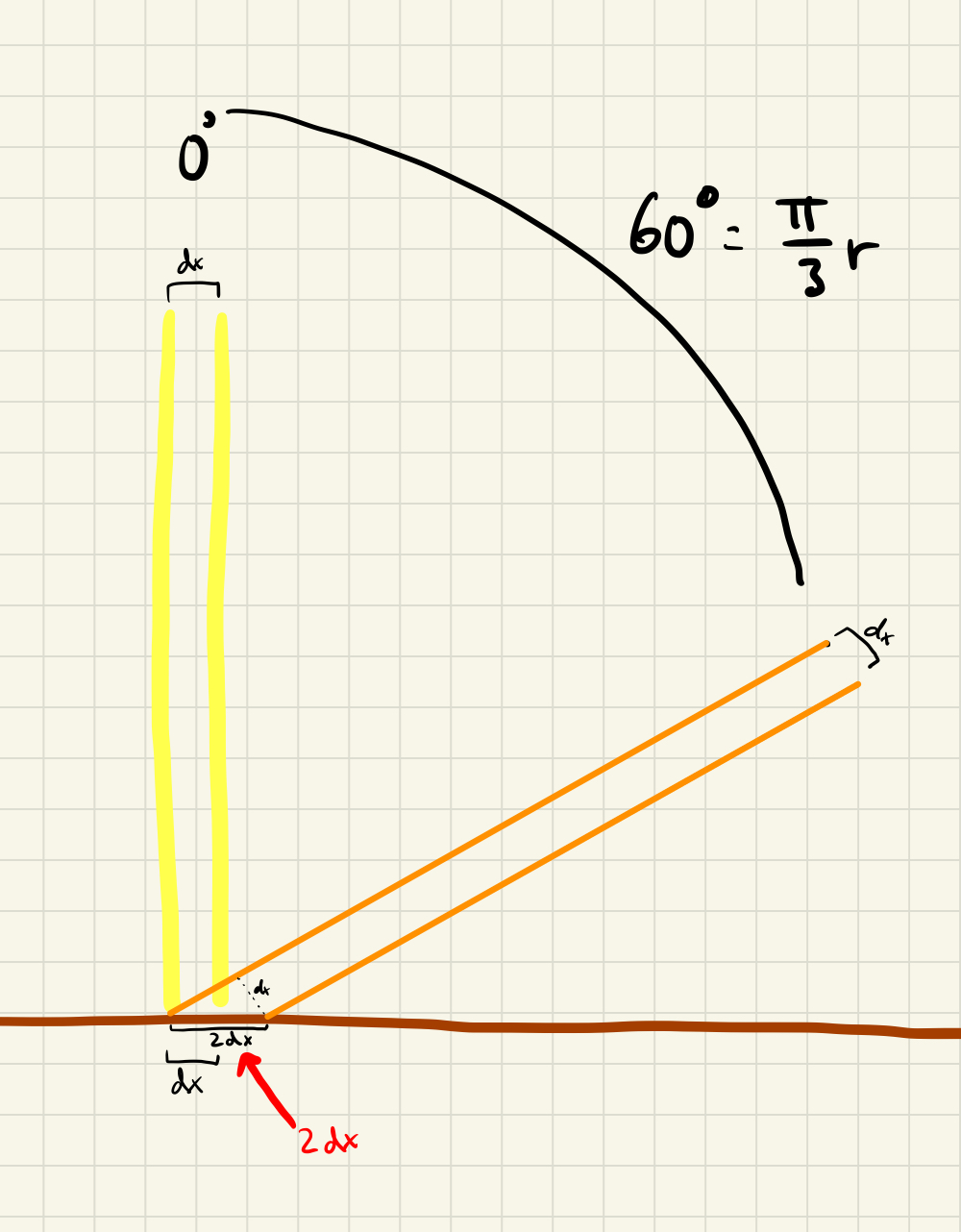
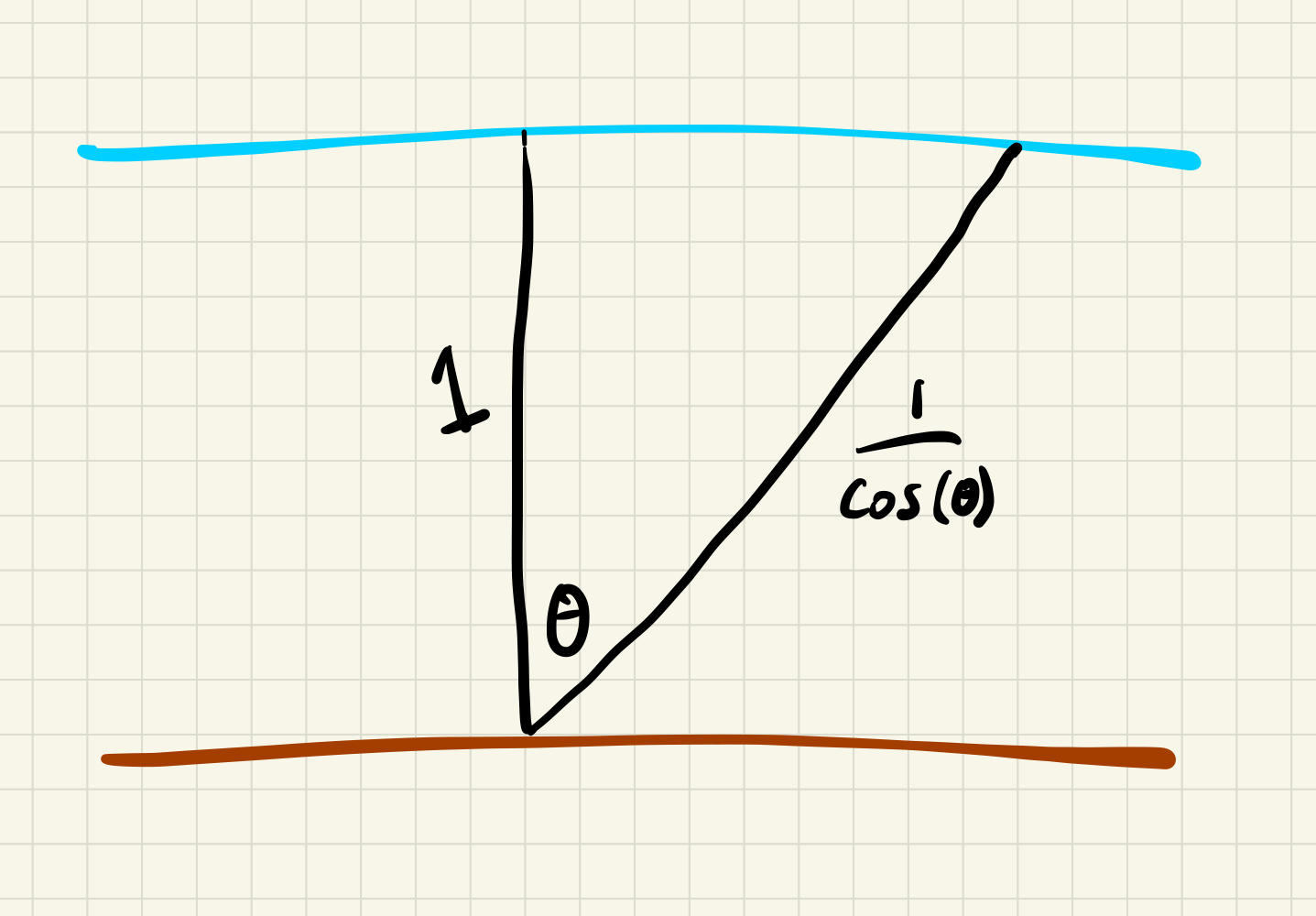
Next we need a formula for the distance of atmosphere sun travels through by solar zenith angle \(\theta\). For this we will use another approximation. The atmosphere is so close to the earth’s surface that we can basically ignore the fact that the earth is a sphere and instead treat it as flat. We have something like this:
So, treating the atmosphere as a straight horizontal line at a height of 1, we can derive that the distance light travels through the atmosphere at a solar zenith angle \(\theta\) is simply \(\frac{1}{cos(\theta)}\).
Next, we use the fact that only \(0.03\) of UV radiation makes it through the atmosphere at noon (distance of 1), to come up with the fact that the amount of UV that makes it through the atmosphere at a solar zenith angle of \(\theta\) is \(0.03^{\frac{1}{cos(\theta)}}\).
Lastly, we need to take into account point #1 which is that light is more direct and therefore intense at noon vs. other times. This one is also not hard to derive with pen and paper, but incidentally has a name: Lambert’s cosine law. It turns out that the amount of light that hits a fixed amount of ground is proportional to \(cos(\theta)\).
Putting it all together, we have the following formula for UV radiation as a function of solar zenith angle \(\theta\):
\[0.03^{\frac{1}{cos(\theta)}} cos(\theta)\]How did we do?
To evaluate this simple model, I evaluated it against NILU’s (Norwegian Institute for Air Research) fastrt model which, at least to my eye, looks extremely sophisticated.
I asked it to compute UV doserates at many different solar zenith angles (with an ozone column of 300 DU) and plotted the results against our model:
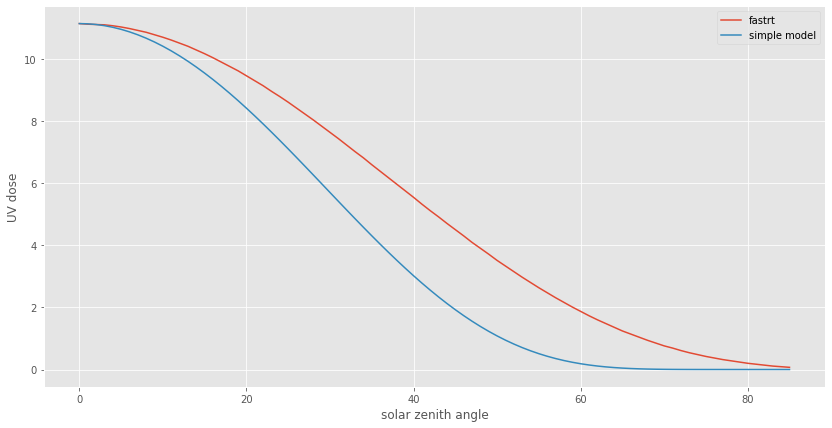
Not terrible! But also not amazing. Our model drastically understimates the amount of UV radiation at larger solar zenith angles relative to noon.
You may be surprised to see this simple model perfectly lines up with fastrt’s model at noon. Well, that’s no coincidence. Notice that our model makes no absolute predictions; it only predicts the amount of UV radiation at a given solar zenith angle relative to noon. So, in order to compare fastrt against our simple model, I set the noon values to be equal.
What account for this discrepancy? Surely many small factors, but I was wondering if there was single major factor that explained a large amount the error. So, I cold emailed the authors of fastrt and they were kind enough to respond!
Our model only takes into account direct solar radiation. But much of the solar radiation that reaches the ground has been scattered by bouncing off things in the atmosphere, only to reach the ground by a much more indirect route. Although I don’t have a quantitative model to back this up, it seems intuitive that the difference between scattered radiation at noon and scattered radiation later in the day would be much less extreme than the difference between direct radiation at those times. Taking scattered radiation into account would increase the relative amount of radiation later in the day.
While we have the data…
We might as well answer a few practial real-life questions. And in order to answer them, I’m going to refer to the following two graphs. These graphs use the UV by solar zenith angle data from fastrt. In order to convert angles to times, I’m assuming that sunrise is at 6am, sunset is at 6pm, and the solar zenith angle increases linearly between those two times.
How much stronger is the sun at noon vs. 2pm?
To answer this, we just refer to the UV dose by time of day graph. At noon, UV does is about 11.13 while at 2pm (14) UV does is 7.63. So almost 50% stronger!
If you’re out in the sun from 10am-2pm, what fraction of the total sun’s UV dose are you receiving?
To answer this, refer to the cumulative UV dose graph. At 10am, the cumulative UV dose so far is 18% of the total. At 2pm (14), it’s 83%. So 65% of the day’s total UV dose happens between 10 and 2.