Will the cosmic microwave background ever disappear?
For those of you who are unfamiliar, the cosmic microwave background, or CMB for short, is radiation from a moment about 400,000 years after the big bang. Before that time, for reasons that I don’t fully understand, the universe was so hot that photons were not able to travel freely through space. Space itself was opaque to light. That by itself is a bit of a mind-bender, but it’s not the mind-bender that I’m after in this post, so just accept it at face value.
I don’t think this is a valid inference to make, but since light could not propagate freely before that time, let’s imagine that the universe was pitch black. Then, in an instant, everything let out a burst of light. Things continued to shine and radiate light after that point, but what we consider the CMB is only that initial burst of light.
The CMB was discovered in the 1960’s and has continued to be measured to this day. I’m here to ask
- How are we still receiving light from 400,000 years after the big bang (over 13 billion years ago)? and
- Will it ever stop?
Let’s start our journey with a less interesting, but much simpler, example:
A flash of light in a static universe
In this and all future thought experiments, I’m going to consider a 1 dimensional universe. A simple straight line. Line-land, if you will. This will greatly help in being able to visualize what we’re talking about. In addition, to make the math simple, I’m going to institute a new speed of light (\(c\)) of 1 meter per second. This will allow us to talk about small, whole number, distances instead of absurdly large ones.
Another simplification that we’re going to make for this particular example is that of a static universe, i.e. one in which space itself is not contracting or expanding.
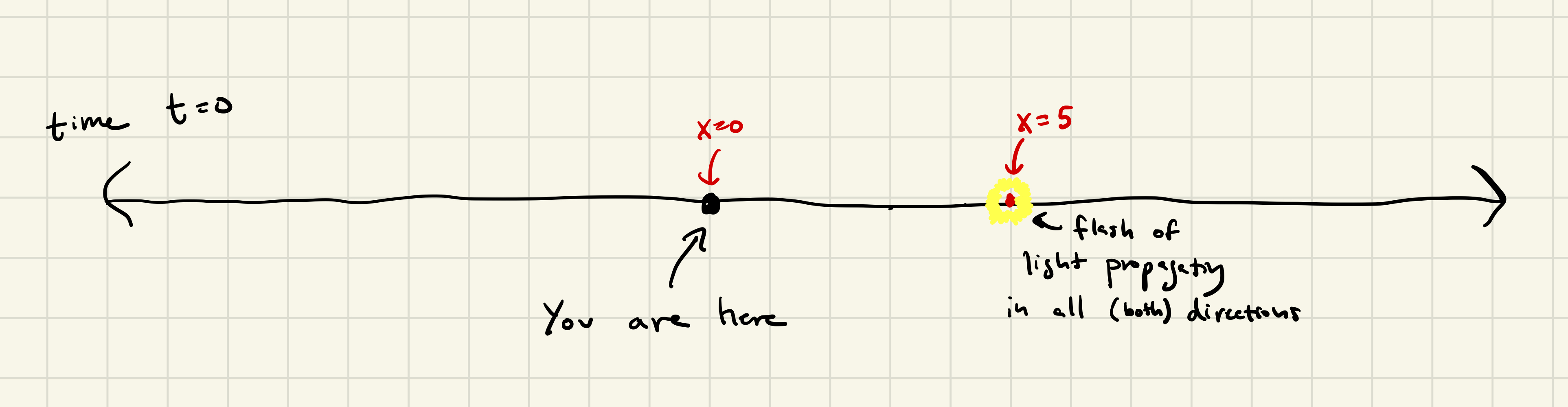
Enough preamble, let’s consider what happens when there is a sudden flash of light at a distance of 5 meters from us. The real-life analogy to this might be a burst of light from some supernova in space. At time \(t = 0\), you cannot see the light as it takes time for the light to propagate from the source of the burst (at \(x = 5\)) to you (at \(x = 0\)).
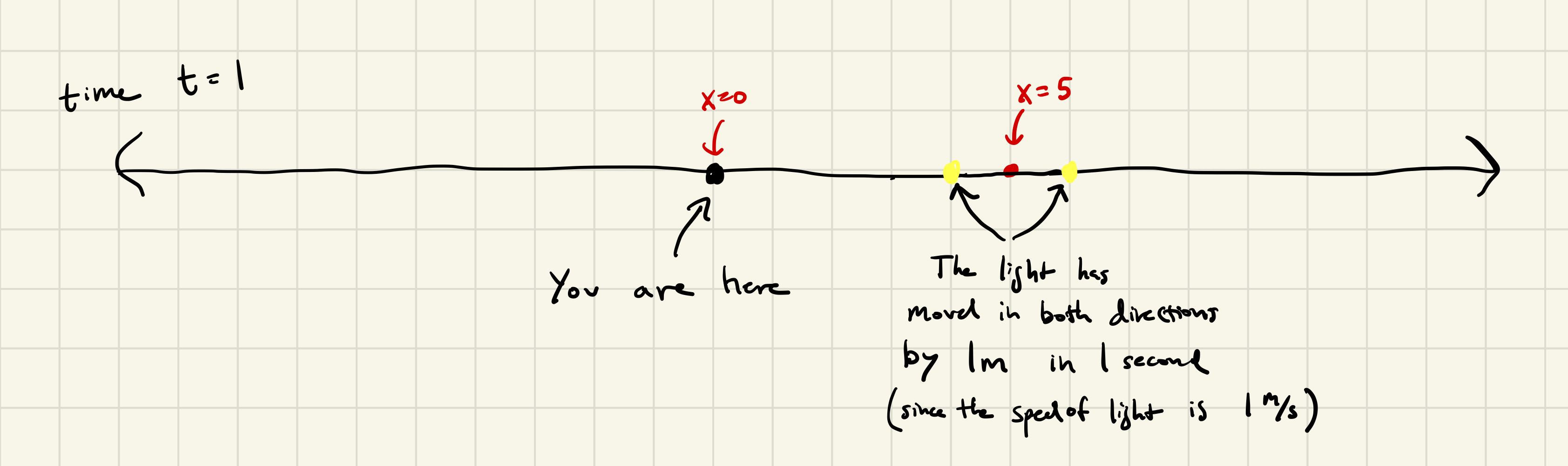
At time \(t = 1\), you still cannot see the flash of light. The light has traveled 1 meter away from the source (at \(x = 5\)) (since, in this universe, light travels at a speed of 1m/s and one second has elapsed), but it has not yet made it all the way to you at \(x = 0\).
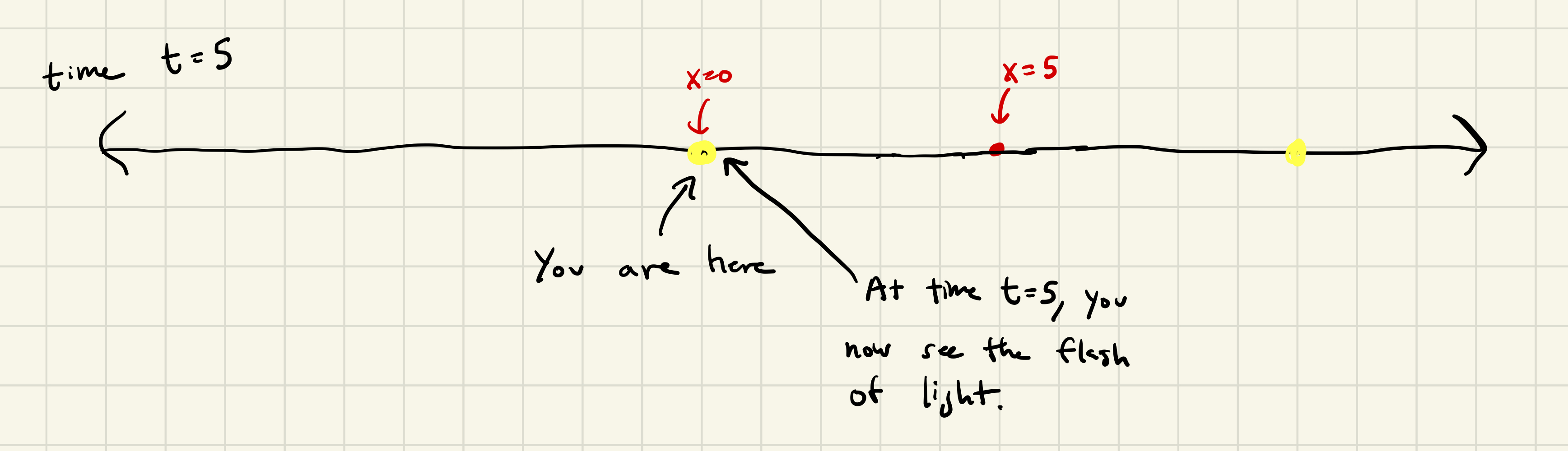
Finally, at time \(t = 5\), the light that left the source 5 seconds ago reaches your eyes. You’re looking into the past and seeing something that happened 5 seconds ago.
The CMB in a static universe
With that simple example out of the way, let’s consider the case of what the CMB would look like in a static universe. The main difference between this example and the previous one is that the flash of light (the CMB) happened at all points in space. So, unlike our flash of light which originated only from \(x = 5\) and propagated outwards from there, the CMB was a flash of light that originated from all \(x\).
Here’s a picture for time \(t = 0\).
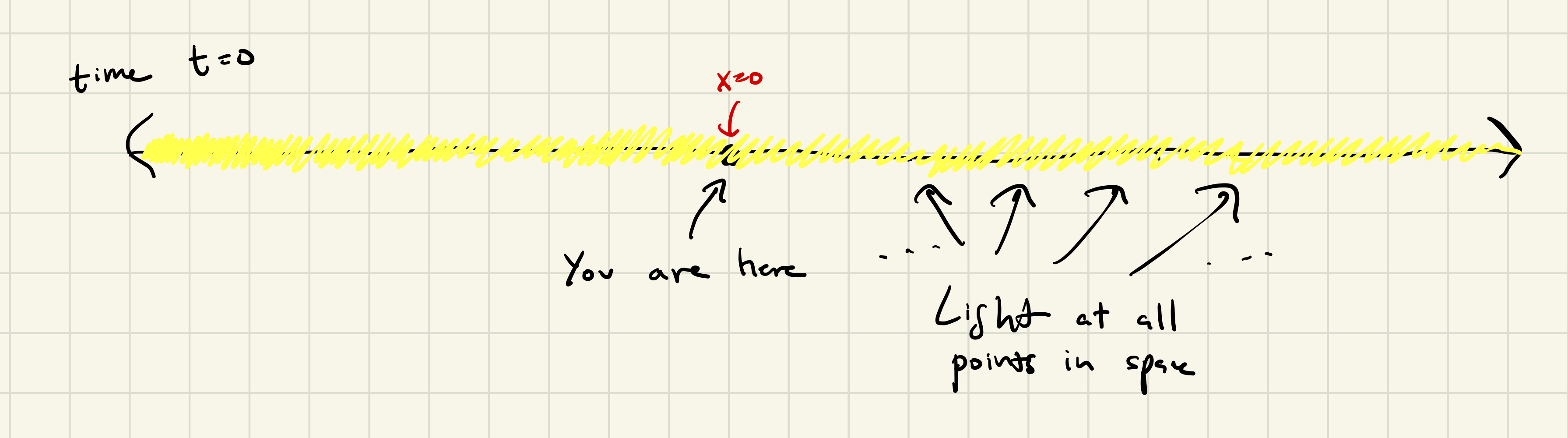
However, for reasons that I hope will become clear, I’m going to redraw that picture in a funny way. For one, I’m going to add time as a second dimension to the graph so that we can see, in a single picture, what is happening over many points in time. Second, instead of drawing all the light in yellow, I’m going to draw the light in each 1-meter section in a different color. This way, we can visually track what a particular section of light does over time. For now, I’ve only filled in what happens to the light from the CMB at time \(t = 0\) (and for the x-range \([-5,5]\)).

Now, let’s fill the picture for the next time slice, \(t = 1\). As you can see, the light propagates towards the viewer (you, at \(x = 0\)) at the speed of, well, light (which, again, is 1m/s in our made-up universe). Note that light also propagates in the other direction (away from \(x = 0\)), but I’ve chosen to omit that so that our picture is less cluttered.

And when we fill in all time slices up to \(t = 5\), the pattern becomes clear.

So, in this example, if you’re an observer at \(x = 0\), you will continually see light from the CMB. The light you see at time \(t\) is light that originated \(t\) meters away from you at time \(t = 0\). Since light was emitted from everywhere at the birth time of the CMB (400,000 years after the big bang), at any point in time \(t\), there will be light that was originally at \(x = t\) and is now at \(x = 0\), just hitting your eye.
But wait, doesn’t that only work if the universe is infinite? If the universe were finite, then at some point you’ll have seen “all” the light from the CMB, right?
Yes! But for now, let’s ignore that. As our examples get more realistic, the infinite universe assumption will no longer be required.
A flash of light in an expanding universe
In this example, we will no longer consider the universe to be static. The current consensus is that the universe is expanding in a very interesting way. It’s expanding such that the distance between any two points grows at a rate that is proportional to the current distance. The canonical way to explain this is to consider a loaf of bread with raisins in it. As the bread cooks, it expands in all directions, such that the distance between any two raisins increases at a rate that’s proportional to the amount of bread (read: space) between them. A picture is probably easier to understand:
What’s the rate of expansion in our made-up universe? Let’s make one up. For simplicity’s sake, let’s pick an instantaneous rate of expansion of 20% per second. That is to say, the line segment \([0,5]\) grows at an instantaneous rate of 1m/s. The line segment \([0,10]\) grows at an instantaneous rate of 2m/s.
With this new property of our universe, let’s revisit our initial example of a flash of light at time \(t = 0\) from a source located (initially) at \(x = 5\). Here again is our starting picture from the “a flash of light in a static universe” example, as nothing has changed (yet):

After one second, however, the picture looks very different! The light is still at a distance of \(x = 5\), the same distance as where it started. The source of light, on the other hand, has moved (away from you, due to the expansion of space).

Note that the numbers in the above picture are approximate. The source would not actually be at exactly \(x=6\) since the rate of change of 20% is an instantaneous rate. Instead it would be at \(x = 5e^{0.2} \approx 6.107\).
Drawing more pictures in this instance is futile. The light has not moved and will never move. We’ve reached what’s called a “fixed point” solution, which is particularly apt in this context, because the point of light is… fixed. As time changes, the distance between you and the beam of light does not.
However, it might be worth considering a different point before moving on from this example. What if the source of light was not initially at \(x = 5\) but rather at \(x = 4\)?
Before stepping through that example, I’m going to take a quick detour. How do we mathematically determine the position of the light at any given point in time? What we know is:
- the initial position of the light
- how the position changes over time
Putting these two facts together, we can produce what’s called a differential equation (because we talk about “differences” (or changes) in \(x\)).
\[\begin{align*} x &= 4 \\ \frac{dx}{dt} &= 0.2x - 1 \end{align*}\]The second equation expresses the fact that space expands at a rate of 20% (\(0.2x\)) while light travels at a speed of 1m/s. These two forces work in opposite directions, which is why they’re subtracted from one another. The expansion of space pushes the light farther and farther away from \(x = 0\) while the fact that light moves through space brings the light closer to \(x = 0\). As an aside, it’s now very easy to see why starting at a value of \(x = 5\) produced a fixed point: because \(\frac{dx}{dt} = 0.2(5) - 1 = 0\)!
Now that we can mathematically represent the motion of the particle of light through space and time, we can compute and graph it:

If you’ve never seen a space-time diagram before, it’s worth spending a bit of time on this picture. On the y-axis is time and on the x-axis is space (or position). Our light blue line represents the position of a particular point of light at many points in time. At time \(t = 0\), the light is at \(x = 4\), and at time \(t \approx 8.04\), the light reaches us at \(x = 0\).
The CMB in an expanding universe
This last step won’t come as a surprise; we want to consider the example of the CMB in an expanding universe. Remember, the only difference between a flash of light and the CMB is that with the CMB, the flash of light happens at all points in space. So, let’s reproduce our graph from above, but instead of only graphing the light beam that started at \(x = 4\), let’s include many starting positions.

With this picture, the story becomes clear (I hope!).
- Light from the CMB travels towards us from all points in space
- We only ever see light that originated in the range \(-5 < x < 5\)
- As the starting position increases, the amount of time it takes for that light to reach us increases non-linearly.
- As the starting position approaches \(x = 5\) (or \(x = -5\)), the amount of time it takes for that light to reach us approaches infinity!
And therefore, our answers to our original two questions are:
- How are we still receiving light from 400,000 years after the big bang (over 13 billion years ago)? Due to the expansion of space, light emitted from a finite distance away can take arbitrarily long (infinitely long, really) to reach us.
- Will it ever stop? No!
Why stop there?
Staring at the last graph can elucidate about some rather mind-bending points:
- We see things from far away in slow motion.
If there were no expansion of space, it would take exactly 0.5 seconds to receive all the light that originated from the range \([4, 4.5]\). However, as we can see from when the light blue and pink lines hit \(x = 0\), those events happen at times \(t \approx 8.04\) and \(t \approx 11.51\) respectively. It takes almost 3.5 seconds to receive that light.
If instead of the CMB, we were watching light from a receding star, the story would be similar. Let’s say at time \(t = 0\) the star was at \(x = 4\). If the only source of motion were the expansion of space, then the star would reach \(x = 4.5\) at time \(t \approx 0.6\), a difference of 0.6s.
We know from our last graph that the light originating from \(x = 4\) at time \(t = 0\) will reach us at time \(t \approx 8.04\). The light originating from \(x = 4.5\) at a time of \(t \approx 0.6\) will reach us 11.51 seconds later, or at time \(t = 12.11\). So we will “watch” this star age 0.6s over the course of about 4 seconds (\(12.11 - 8.04\)). In other words, we will see it age in slow motion.

- Nothing ever disappears, it only freezes in time.
If we let our story continue, it only gets stranger. Our receding star will reach \(x = 4.9\) at a time of \(t \approx 1\), and when it emits light, that light will reach us at time \(t \approx 20.5\). Our star will reach \(x = 4.99\) at time \(t \approx 1.1\), and that light will reach us at \(t \approx 32\). It will reach \(x = 4.9999999999\) at a time \(t \approx 1.11\) and that light will reach us at \(t \approx 124\). And so on!
Even though the star will cross our “fixed point” (event horizon) of \(x = 5\) at \(t \approx 1.11\), we will never see that happen. Instead we will see it get closer and closer to \(x = 5\), and each incremental step towards \(x = 5\) will take progressively longer and longer. Eventually the star will appear to freeze in time (and space).
Due to the fact that a finite amount of light will (in the limit) be spread over an infinite amount of time, the star will get dimmer and dimmer, redshifted out of existence. Nothing ever leaves us, it just fades away. How poetic.