Fractional Derivatives
What’s the \(\frac{1}{3}\)rd derivative of \(sin(x)\)?
What an absurd question - does it even make sense? I think so, but in order to build up some intuition let’s take a few steps back.
Imagine that you lived in the middle ages and you were comfortable with the concepts of addition and multiplication. You even understand exponents, as a shorthand for repeated multiplication. Then someone asks you, what’s \(2^{\frac{1}{2}}\)?
Nonsense, right? \(2^3\) means \(2 \cdot 2 \cdot 2\). There are three twos. You can’t have half a two.
Well, as I’m sure you know, yes - you can. But think about it for a second. What does it mean? What does it mean to multiply by \(x\) half a time?
\(x^n\) is the number that you get when you multiply \(x\) \(n\)-times. Thinking about it this way makes the property \(x^a \cdot x^b = x^{a+b}\) obvious. If you multiply by \(x\) \(a\) times, and then \(b\) more times, you’ve multiplied by \(x\) \((a+b)\) times. And that property is nice, because it makes sense even when \(n\) is not an integer. If I do something \(\frac{1}{2}\) a time and then I do it again \(\frac{1}{2}\) a time, how many times have I done it? \(1\) time, right?
Which brings us to the (obvious because we already learned it) answer, which is that \(2^{\frac{1}{2}} \cdot 2^{\frac{1}{2}} = 2^1 = 2\), i.e. \(2^{\frac{1}{2}} = \sqrt{2}\).
Let’s generalize a bit and talk about repeated function application.
Consider the function \(f(x) = x + 10\). What’s \(f(f(x))\)? That’s pretty easy:
\[f^2(x) = f(f(x)) = f(x+10) = x+20\]Ok, how about \(f^{\frac{1}{2}}(x)\)? Given the setup, I bet you can figure it out. It’s some function that, when applied twice, gives us \(f(x)\). What might that be? \(g(x) = x+5\) seems like a good guess.
Let’s check it:
\[\begin{align*} f^{\frac{1}{2}}(x) &= g(x) = x + 5 \\ g(g(x)) &= g(x+5) = x+10 = f(x) \end{align*}\]Ok, how about another this one? If \(f(x) = 2x\), what’s \(f^{\frac{1}{2}}(x)\)? Again, you can guess it. It’s \(g(x) = \sqrt{2}x\).
Alright, now let’s level up. Previously we were dealing with functions from a number to a number, but functions can take other types of things too. How about a function \(f\) which takes, as input, a function \(h\) and returns a new function? What does it do to the function? Let’s start with something easy, like it shifts it \(10\) to the right:
\[f(h(x)) = h(x - 10)\]Can we guess the answer for \(f^{\frac{1}{2}}(x)\)? I’m going to go out on a limb and say yes. If you want to do something twice such that the end result is shifting \(10\) to the right, shifting \(5\) to the right each time will probably do the trick.
\[\begin{align*} f^{\frac{1}{2}}(h(x)) &= g(h(x)) = h(x-5) \\ g(g(h(x))) &= g(h(x-5)) = h(x - 10) \end{align*}\]Ok, now for the finale. What if our function takes the derivative of the input function? In other words:
\[f(h) = \frac{d}{dx}h\]Eek… that is a bit harder.
Let’s take a quick detour and draw an analogy to linear algebra, specifically eigenvectors. If you want to multiply a vector, \(v\), by a matrix, \(M\), \(n\) times (where \(n\) is sufficiently large), a fast way to do it is to follow these three steps:
- Compute the eigenvectors of the matrix \(M\). These are the vectors that, when multiplied by \(M\), are just scaled by a constant (the constant being the eigenvalue).
- Decompose your vector into a linear combination (weighted sum) of those eigenvectors.
- Your answer is the linear combination of those eigenvectors, where each eigenvector is first scaled by its eigenvalue to the \(n\)th power.
I tried to explain why this works in depth here, but the quick summary is that we found special inputs (the eigenvectors) which were particularly easy compute for our function (multiplication by \(M\)), and then we reformulated our answer as a weighted sum of the function applied to those special inputs (\(n\) times). In doing so, we turned our somewhat hard problem into a much easier one.
One thing to mention is that this only work for linear functions, i.e. functions \(f\) which have the following two properties:
- \[f(u + v) = f(u) + f(v)\]
- \[f(\alpha u) = \alpha f(u) \tag{where $\alpha$ is a scalar}\]
Does the derivative function have these properties? Actually yes:
- \[\frac{d}{dx}(f + g) = \frac{d}{dx}(f) + \frac{d}{dx}(g)\]
- \[\frac{d}{dx}(\alpha f) = \alpha \frac{d}{dx}(f) \tag{where $\alpha$ is a scalar}\]
The derivative is a linear function (often called a linear operator). So, we can utilize the same trick.
Can you think of any functions which have a derivative that are equal to the function itself (or, maybe, a scaled version of it)?
Yep, you bet: \(\frac{d}{dx}(e^x) = e^x\), and \(\frac{d}{dx}(e^{\alpha x}) = \alpha e^{\alpha x}\).
\(e^{\alpha x}\) is an eigenfunction of the derivative function. How cool!
So, if we could represent our input function \(h\) as a weighted sum of exponential functions, then we can trivially take the derivative any number of times (where that number doesn’t have to be an integer).
Oh, what’s that you say? The fourier transform can convert any function into a integral (read: weighted sum) of complex exponential functions (sometimes called complex sinusoids)?
\[\begin{align*} \hat{f}(\omega) &= \int_{-\infty}^{\infty} f(x) e^{-2 \pi i x \omega } dx \\ f(x) &= \int_{-\infty}^{\infty} \hat{f}(\omega) e^{2 \pi i x \omega } d\omega \\ \end{align*}\]So, we’ve rewritten our function as a weighted sum of eigenfunctions of the derivative operator. The weights are \(\hat{f}(\omega)\) and the eigenfunctions are \(e^{2 \pi i \omega x}\). So, now we can trivially1 take the \(n\)th derivative:
\[\frac{d^n}{dx^n} f(x) = \int_{-\infty}^{\infty} (2 \pi i \omega)^n \hat{f}(\omega) e^{2 \pi i x \omega } d\omega \\\]At this point, we’ve solved how to take the \(n\)th derivative in the general case, but we haven’t technically answered our original question: what’s the \(\frac{1}{3}\)rd derivative of \(sin(x)\)?
Lucky for us, the fourier transform of \(sin(x)\) is quite simple. To get a handle on it, let’s first graph \(f(t) = e^{it}\). Unfortunately, since \(e^{it}\) is a complex number for a given \(t\), in order to graph the function for a range of \(t\) values I’d need 3 dimensions. So, instead, I’ll graph \(e^{it}\) as a function of time (time will by my 3rd dimension).
So that’s a single complex exponential function. What if we add one more which rotates at exactly the same rate but in the opposite direction, and then add the two values together?
The imaginary (vertical) components cancel each other out perfectly and all we’re left with is a real number, which is twice a \(sin\) curve.
Analytically,
\[f(x) = sin(x) = \frac{1}{2} (-i e^{ix} + i e^{-ix})\]Why multiply \(e^{ix}\) by \(-i\) and \(e^{ix}\) by \(i\)? Since \(sin\) starts at 0, I want the counter-clockwise complex exponential (\(e^{ix}\)) to start out pointing down (and multiplication by \(-i\) will rotate clockwise by \(\pi/2\). Similarly, I want the clockwise one (\(e^{-ix}\)) to start out pointing up (and multiplying by \(i\) will do that).
Let’s test our function for a few values of \(x\):
\[\begin{align*} sin(0) &= \frac{1}{2} (-i e^{i0} + i e^{-i0}) = \frac{1}{2} (-i + i) = 0 \\ sin(\pi/2) &= \frac{1}{2} (-i e^{i\pi/2} + i e^{-i\pi/2}) = \frac{1}{2} (-i \cdot i + i \cdot -i) = \frac{1}{2} (1 + 1) = 1 \\ sin(\pi) &= \frac{1}{2} (-i e^{i\pi} + i e^{-i\pi}) = \frac{1}{2} (-i \cdot -1 + i \cdot -1) = \frac{1}{2} (i + -i) = 0 \\ sin(3\pi/2) &= \frac{1}{2} (-i e^{i3\pi/2} + i e^{-i3\pi/2}) = \frac{1}{2} (-i \cdot -i + i \cdot i) = \frac{1}{2} (-1 + -1) = -1 \\ \end{align*}\]So far so good. How about its derivative?
\[\begin{align*} \frac{d}{dx}sin(x) &= \frac{d}{dx} \big( \frac{1}{2} (-i e^{ix} + i e^{-ix}) \big) \\ &= \frac{1}{2} (e^{ix} + e^{-ix}) \end{align*}\]Well, we know what it should come out to, \(cos(x)\). Does it?
Yes, and here’s one way to think about it (you could also plug in a few values of \(x\) to really convince yourself). The form of this equation looks similar to the form of our equation for \(sin(x)\), except that the two complex exponential functions aren’t multiplied by \(-i\) and \(i\), respectively. That just means they both start out pointing directly to the right, instead of one pointing down and one pointing up like in the \(sin(x)\) case. You can look at the animation above and verify for yourself that if you start watching when the red and blue components are both pointing right, the graph looks like a \(cos(x)\) curve.
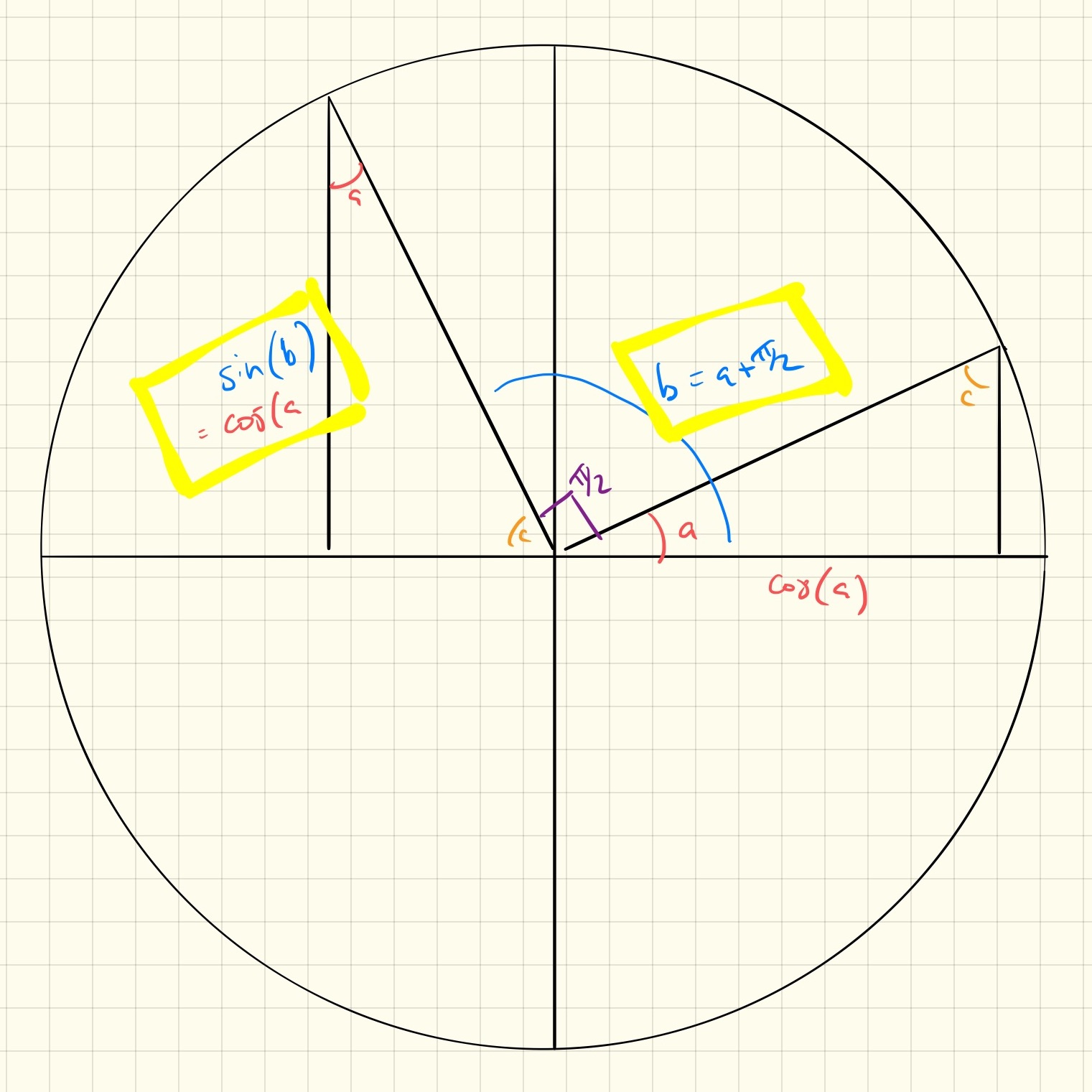
What this also makes apparent, though, is that \(cos(x)\) and \(sin(x)\) are generated by the same process, it’s just that \(cos(x)\) is just \(\pi/2\) “ahead” of \(sin(x)\). This probably sounds familiar - that \(sin(x + \pi/2)\) and \(cos(x)\) are the same thing. One easy way to prove to yourself that this is to consider the fact that \(cos(a) = sin(b)\) in the (left) right triangle below and that \(b = a + \pi/2\).
Ok, this interesting and all, but let’s solve the problem.
\[\begin{align*} \newcommand{\d}{\frac{d^{1/3}}{dx^{1/3}}} \d sin(x) &= \d \big( \frac{1}{2} (-i e^{ix} + i e^{-ix}) \big) \\ &= \frac{1}{2} (-i \cdot i^{1/3} e^{ix} + i \cdot (-i)^{1/3} e^{-ix}) \\ &= \frac{1}{2} (-i \cdot e^{i \frac{\pi/2}{3}} \cdot e^{ix} + i \cdot e^{i \frac{-\pi/2}{3}} \cdot e^{-ix}) \tag{using the fact that $i = e^{i\pi/2}$} \\ &= \frac{1}{2} (-i e^{i(x + \pi/6)} + i e^{-i(x + \pi/6)}) \\ &= sin(x + \pi/6) \\ \end{align*}\]And, in general:
\[\frac{d^n}{dx^n}sin(x) = sin(x + n \pi/2)\]Ok, one last thing (I promise!). We’ve been focusing on fractional derivatives, but how about negative ones? We have a general formula in terms of \(n\), is there anything wrong with taking the derivative “-1” times? Nope! That should just correspond to taking the anti-derivative.
So, in conclusion, the \(\frac{-1}{\pi}\)th derivative of \(sin(x)\) is (obviously) \(sin(x - 1/2)\).
-
Note this is using the mathematician’s definition of trivial, i.e. “theoretically possible” ↩