N-spheres
What’s the formula for the volume of a 4-dimensional sphere? If you have that one, can you come up with a formula for the volume of an n-dimensional sphere?
Don’t look it up! It’s a good problem. I highly encourage you to work on it before looking at my solution.
More specifically, try to come up with an equation which relates the volume of an n-dimensional sphere to an (n-1) dimensional sphere. You may not be able to analytically evaluate your equation yourself (I wasn’t), but it should be something that a computer could solve.
I took the calculus approach and modeled an n-dimensional sphere as an integral of (n-1)-dimensional spheres. I denoted the volume of an n-dimensional sphere as \(f_n(r)\). For a 3-dimensional sphere, my approach corresponds to following picture:
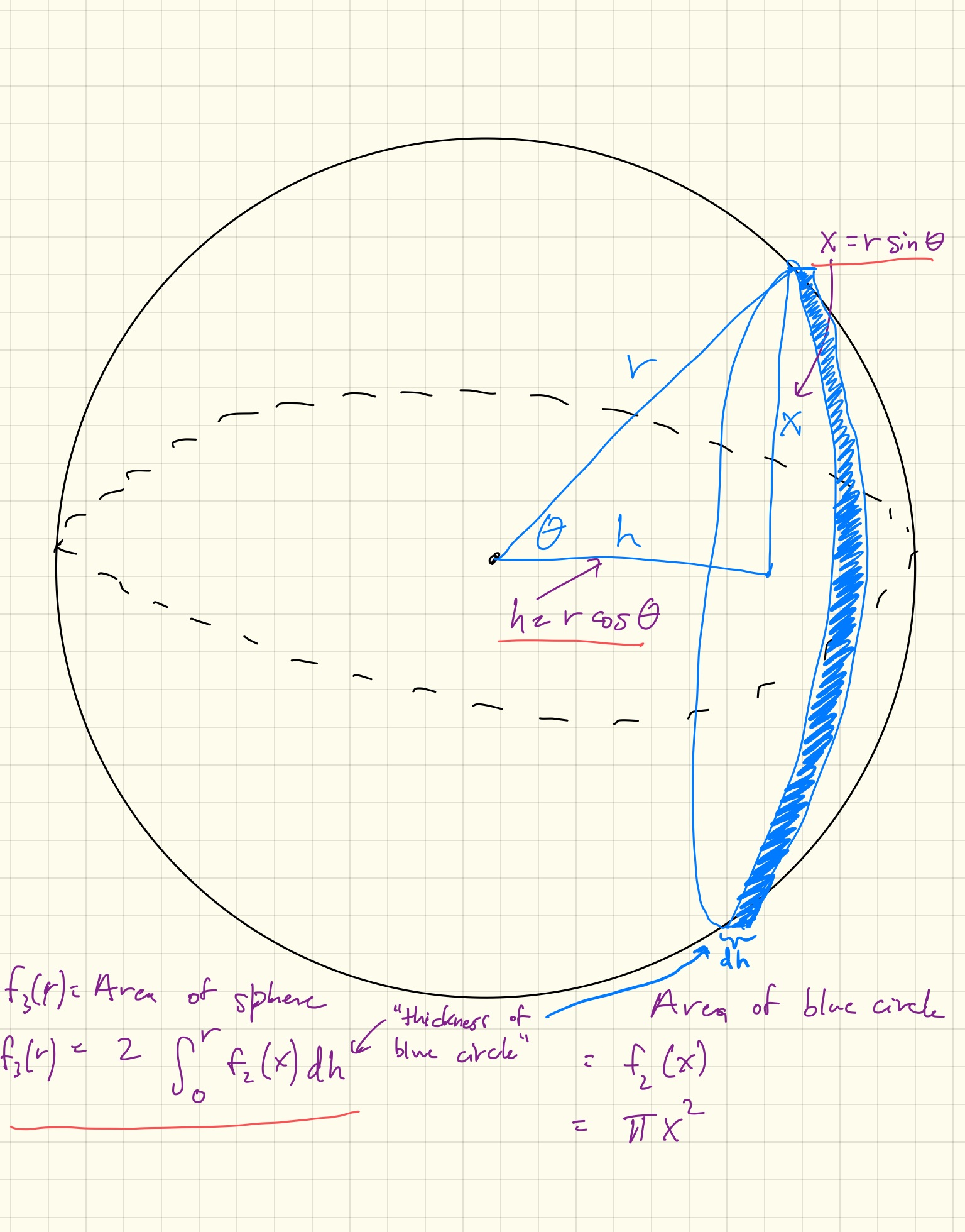
More generally, my recursive formula is the following system of equations:
\[\begin{align*} f_n(r) &= 2 \int_0^r f_{n-1}(x) dh \\ x &= r \sin(\theta) \\ h &= r \cos(\theta) \\ dh &= -r \sin(\theta) d\theta \end{align*}\]which, if you substitute, you get:
\[f_n(r) = 2 \int_{\pi/2}^0 f_{n-1}(r\sin(\theta)) (-r \sin(\theta)) d\theta\]Plugging this integral into python (using sympy), and starting with the formula for the “volume” of a “0-dimensional sphere”, i.e. a point, I was able to recursively derive the formulas I recognized for a circle and a sphere and beyond!
Note the formula for the “volume” of a 0-dimensional sphere (point) is \(f_n(0) = r^0 = 1\).
I tried to find the pattern in these formulas to come up with the closed formula solution, but in the end I gave up and looked at wikipedia, which of course has the solution. I’m not shocked I didn’t find the pattern, it’s non-trivial.
Quick note: The following approach might be a bit more straightforward and also works. However, I couldn’t solve the integral by hand to obtain the (known) formula for a 3-dimensional sphere - and that was how I was checking my work - which is why I went with the approach above.
\[f_n(r) = 2 \int_0^r f_{n-1} \Big( \sqrt{r^2 - x^2} \Big) dx\]