\(\newcommand{\vec}[2]{\left[\begin{matrix}#1\\#2\end{matrix}\right]} \newcommand{\vv}[1]{\overrightarrow{#1}} \newcommand{\norm}[1]{\lVert#1\rVert} \newcommand{\mat}[4]{\left[\begin{matrix}#1 & #3\\#2 & #4\end{matrix}\right]}\)

In the last post, I tried to explain what a tensor is. It’s complicated; it’s a long post. But what I didn’t tackle is the why. Why do we care about this generalization of vectors and matrices?

To be honest, I mostly don’t know yet. My hope is to actually learn the math behind general relatively at some point, and my current understanding is that tensors are part of that math. However, I do have one interesting point to make.

What is the dot product of a vector with itself? It’s the length squared, right?

Take, for instance, the vector \(\vv{v} = [3, 4]\) (with length 5):

\[\vec{3}{4} \cdot \vec{3}{4} = 3 \cdot 3 + 4 \cdot 4 = 25\]

Right, of course this works. We’ve just reformulated the Pythagorean theorem in a linear-algebra sort of way.

But wait, something is odd here. In the last post, we made a big deal about how covectors were different than vectors. covectors were functions from vectors to scalars, not vectors. What does it even mean, then, to multiply two vectors together? In programming terms, it’s like we’ve made a type error.

If we wanted to construct a (multi-linear) function from 2 vectors to a scalar, as we seem to want when taking the dot product of 2 vectors, we’d need a (0, 2)-tensor. Recall, that an (n, m)-tensor is a multi-linear function from m vectors and n covectors to a scalar.

That’s actually correct, and the (0, 2)-tensor that we want is called the metric tensor. To see why, let’s change our basis from the standard orthonormal basis to something else.

Let’s use a new basis of \(\vv{e_1} = [4, 4]\) and \(\vv{e_2} = [-1, 0]\). What are the coordinates of the vector \(\vv{v}\) in the new basis? It looks like \([1, 1]\) will do the trick. How convenient.

Ok, so what’s the length of \(\vv{v}\) now? It’s the same! The length of a vector does not depend on the coordinate system.

Right, right, what I meant was, how do we compute the length of the vector now? Dot product right?

\[\vec{1}{1} \cdot \vec{1}{1} = 1 \cdot 1 + 1 \cdot 1 = 2\]

Uh… that’s not right. No, of course that doesn’t work. The length of the vector has to depend on the length of the basis vectors. What I meant was to first scale each coordinate by the length of the appropriate basis vector before doing the multiplication. Something like this:

\[\vec{1}{1} \cdot \vec{1}{1} = (1 \cdot \norm{\vv{e_1}}) \cdot (1 \cdot \norm{\vv{e_1}}) + (1 \cdot \norm{\vv{e_2}}) \cdot (1 \cdot \norm{\vv{e_2}}) = 1 \cdot 32 + 1 \cdot 1 = 33\]

Hmm, yea not that either. I guess I’m still trying to use the Pythagorean theorem, but my triangle is not a right triangle anymore. I’m making a triangle with one basis vector \(\vv{e_1} = [4, 4]\) and one basis vector \(\vv{e_2} = [-1, 0]\), but those vectors aren’t orthogonal.

All this would be much more clear with a picture:

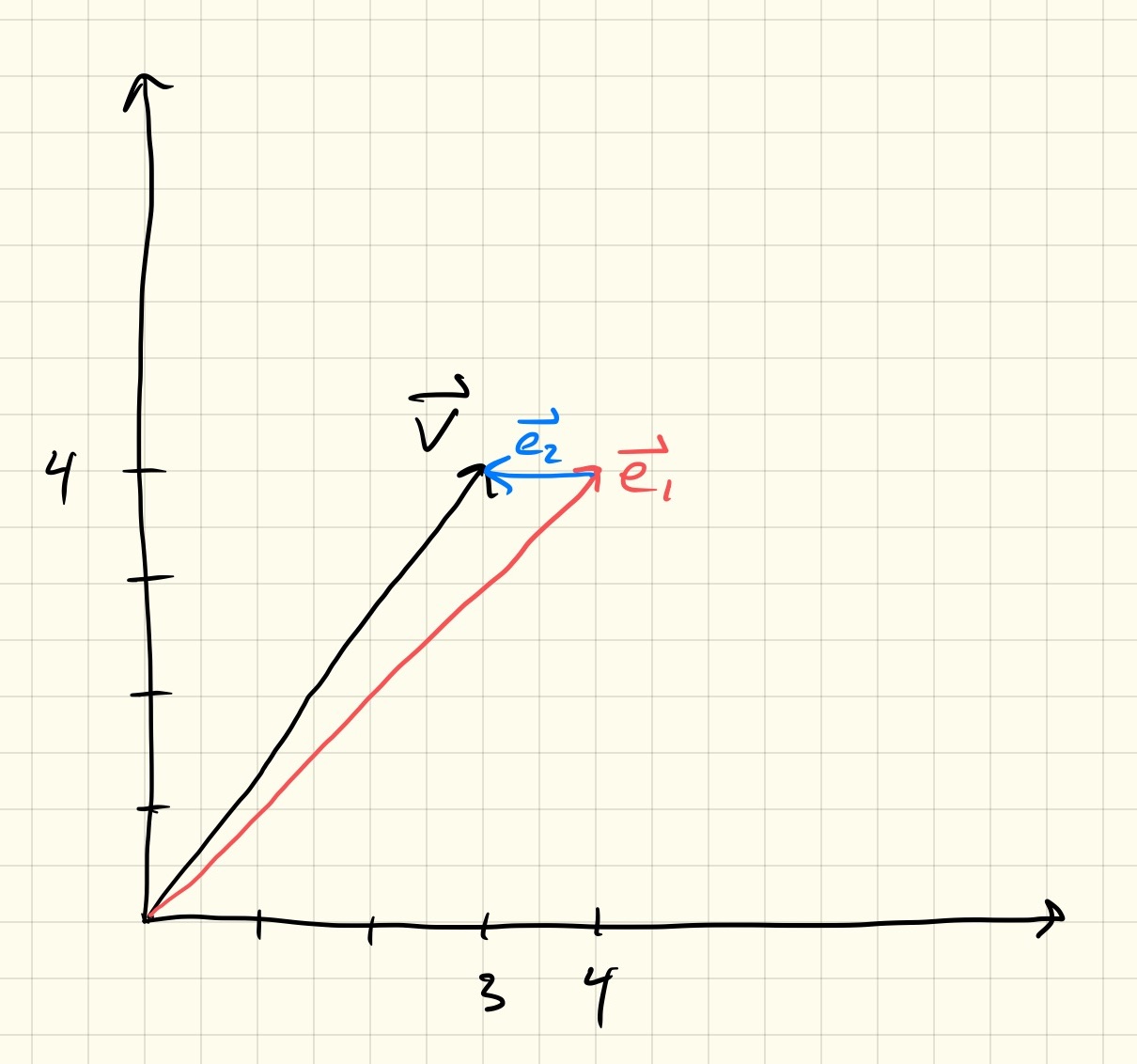
So maybe law of cosines? \(c^2 = a^2 + b^2 - 2ab\cos{C}\)? Actually yes, that’s exactly right, but let me show you another way.

Like I said before, what we want is called the metric tensor.

\[[[ {\vv{e_1}\cdot\vv{e_1}}, {\vv{e_2}\cdot\vv{e_1}} ], [ {\vv{e_1}\cdot\vv{e_2}}, {\vv{e_2}\cdot\vv{e_2}} ]]\]

I wrote it out that way, as a row of row-vectors, on purpose. The metric tensor is a (0, 2)-tensor, meaning it’s a function from two vectors to a scalar, and a row of row vectors has the right dimensionality for that multiplication. Let’s try it out with our new basis:

\[\begin{align*} \vv{e_1} \cdot \vv{e_1} &= 32 \\ \vv{e_1} \cdot \vv{e_2} &= -4 \\ \vv{e_2} \cdot \vv{e_2} &= 1 \\ \end{align*}\]

So, our metric tensor is:

\[[[32, -4], [-4, 1]]\]

Let’s multiply it by our vector \(v = [1, 1]\):

\[[[32 -4], [-4, 1]] \vec{1}{1} = [28, -3]\]

And again?

\[[28, -3] \vec{1}{1} = 25\]

It works! So, why haven’t we ever heard of this thing before? Well, let’s write out the metric tensor in the standard, orthonormal basis:

\[\begin{align*} \vv{b_1} &= [1, 0] \\ \vv{b_2} &= [0, 1] \\ \vv{b_1} \cdot \vv{b_1} &= 1 \\ \vv{b_1} \cdot \vv{b_2} &= 0 \\ \vv{b_2} \cdot \vv{b_2} &= 1 \\ \end{align*}\]

So, the metric tensor, in an orthonormal basis, is the identity function:

\[[[1, 0], [0, 1]]\]

which is why ignoring it, and treating vectors and covectors interchangeably, is usually fine.