Deriving the Taylor Series

My previous post Deriving the Maclaurin Series is a prerequisite for this post.

We’ve just learned how to approximate a function $f (x)$ using the Maclaurin Series. It’s a pretty sweet hammer, so let’s start hitting some nails. How about $e^{x}$ ?

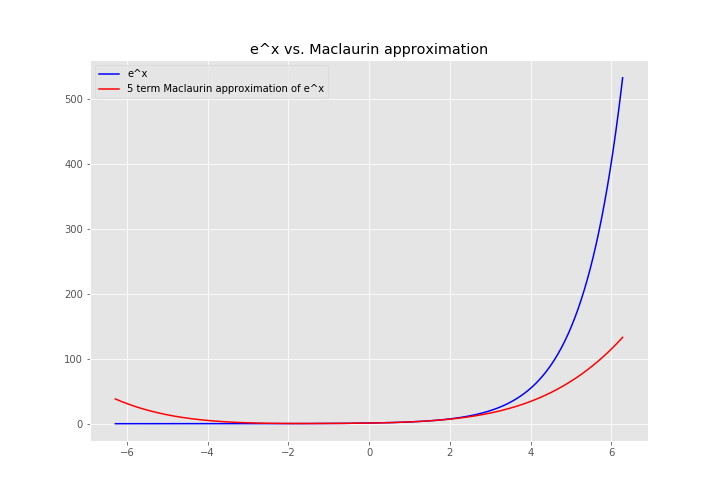
If you care about the region around 0, you’re golden. This is a great approximation. But what if you care about $x = 6$ ? It’s… not great. One option is to add more terms. We used the first 5 terms of the Maclaurin Series. We could use 100. That would definitely work. However, if you know beforehand that you care about a particular region that is not the region around 0, there’s a better way.

When might you know beforehand which x-region you care about in real life? Actually, quite often. Let’s say the function you’re approximating is the percentage humidity in the air as a function of temperature. Are you particularly interested in a temperature of 0? Probably not. You’re probably most interested in temperatures that are close to your current temperature. If you come up with real-life examples, there’s often a natural “default” x value and you probably care most about the x-region around that default value.

So what’s the better way? It’s called the Taylor Series, and it’s just two small steps away from the Maclaurin Series.

Step 1

We want the polynomial $p$ that best approximates a function $f$ around the point $f (a)$ . However, as a first step, we’re first going to solve for a polynomial $p^{'}$ that is almost the polynomial we want. It’s going to be exactly the Maclaurin Series, except in place of $f (0)$ , $f^{'} (0)$ , etc., we’re going to use $f (a)$ , $f^{'} (a)$ , etc. I.e.

p^{'} (x) = f (a) + f^{'} (a) x + \frac{f^{″} (a)}{2!} x^{2} + \frac{f^{‴} (a)}{3!} x^{3} + \dots + \frac{f^{(n)} (a)}{n!} x^{n} + \dots

Because we’re now using the function value (and derivatives) around $x = a$ , the resulting polynomial will look very similar to $f$ around $a$ . The only problem is that it’s still centered around the origin.

A picture is going to be much easier to understand:

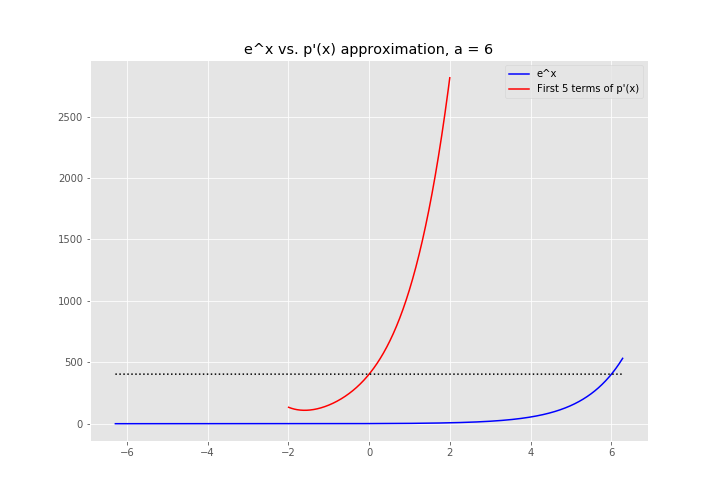
Notice how the red line, $p^{'} (x)$ has the same value and shape around $x = 0$ as $f (x)$ does around $x = 6$ ?

Step 2

This is the easy step, we need to shift our function to the right by $a$ . You may just remember this back from algebra, but if not, we want $p (x) = p^{'} (x - a)$ .

\begin{aligned} p (x) & = p^{'} (x - a) \\ = f (a) + f^{'} (a) (x - a) + \frac{f^{″} (a)}{2!} (x - a)^{2} + \frac{f^{‴} (a)}{3!} (x - a)^{3} + \dots + \frac{f^{(n)} (a)}{n!} (x - a)^{n} + \dots \end{aligned}

And, not that it will surprise you, but here’s the final picture (re-centered around $x = 6$ ):

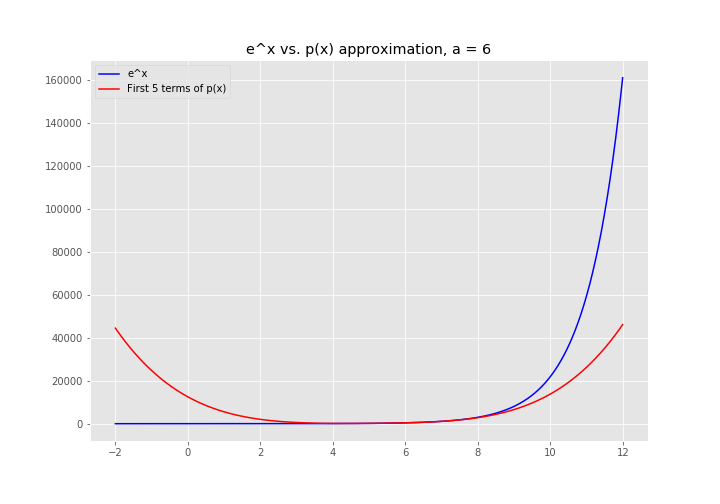
Notice that $p (x)$ is a much worse approximation of $e^{x}$ around $x = 0$ , similar to how the Maclaurin Series was a terrible approximation around $x = 6$ . There’s no magic going on here. We traded off accuracy around $x = 0$ for accuracy around $x = 6$ . If you need more accuracy everywhere, you need more terms.