Through Two Doors at Once
You can think of this post as CliffsNotes for the book Through Two Doors at Once, which I’m currently enjoying reading. It’s actually quite an easy read, in some sense, but I find that to be double-edged given the subject matter (Quantum Mechanics). In my opinion, every once in a while you need to step back and try to distill what you’ve read down into something small and digestible in order to have any chance at absorbing material that is so counterintuitive and absurd. So, that’s what I’m doing here.
Unfortunately for you (the reader), I’m doing this mostly for myself. I’m including just enough information to remind myself of what I’ve read, which might not be enough for you to really follow along. But hey, feel free to ask questions in the comments and I’ll be happy to fill in parts as necessary.
So why include this in a public blog at all if it’s meant for myself? Well, I’m genuinely interested in the answers to my questions at the end. So to the extent that anyone ever reads this and has insight into those questions, I’d love to hear about it in the comments.
#1 Single Slit Experiment: 1 beam splitter
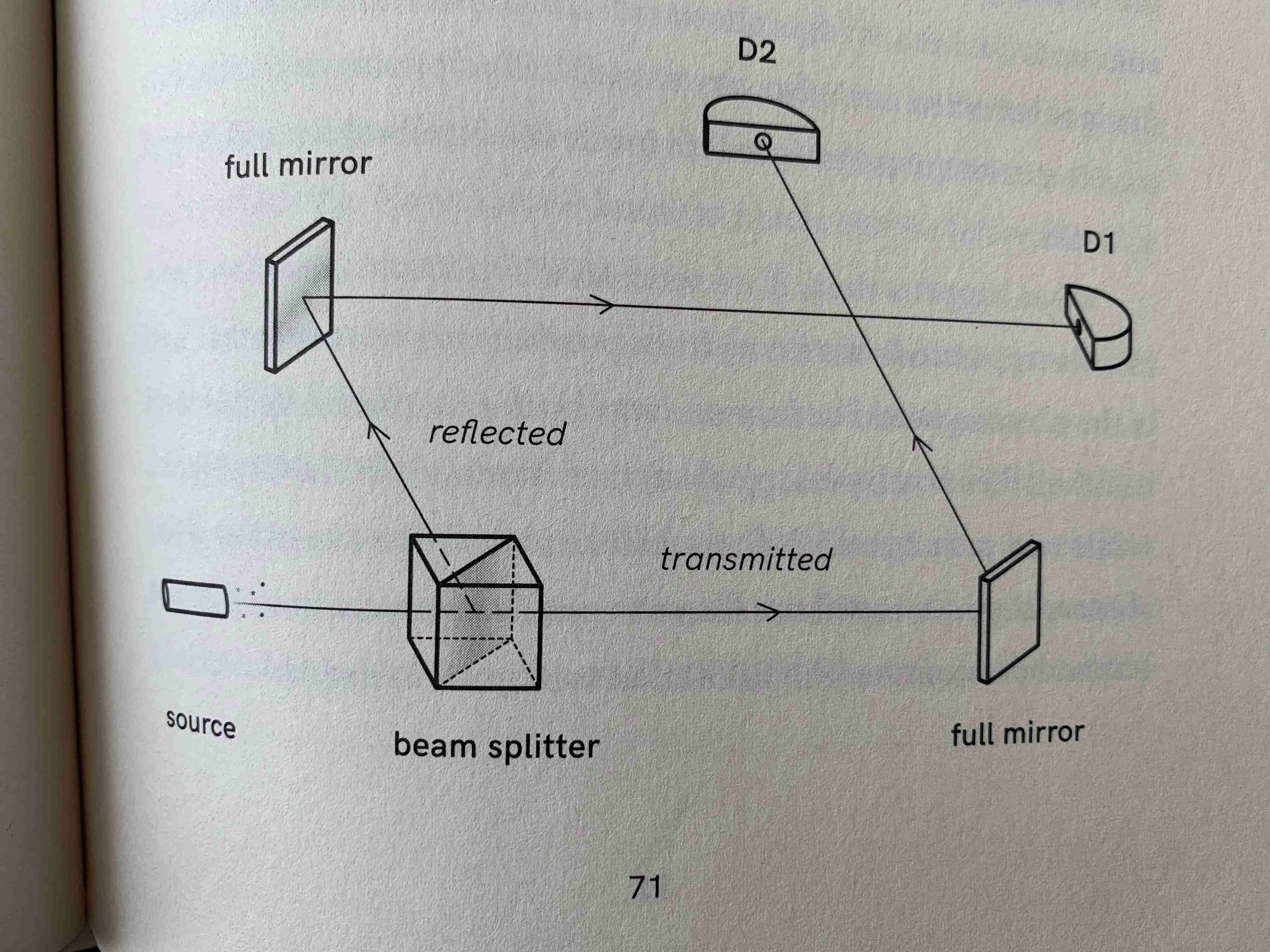
- send 10,000 photons from source
- D1 clicks 5,000 times, and D2 clicks 5,000 times
- Truly random, i.e. for a given photon you can never predict which decector (D1 or D2) it will hit. You can only say that it will hit D1 with probability \(\frac{1}{2}\) and it will hit D2 with probability \(\frac{1}{2}\).
#2 Double Slit Experiment 1: 2 beam splitters
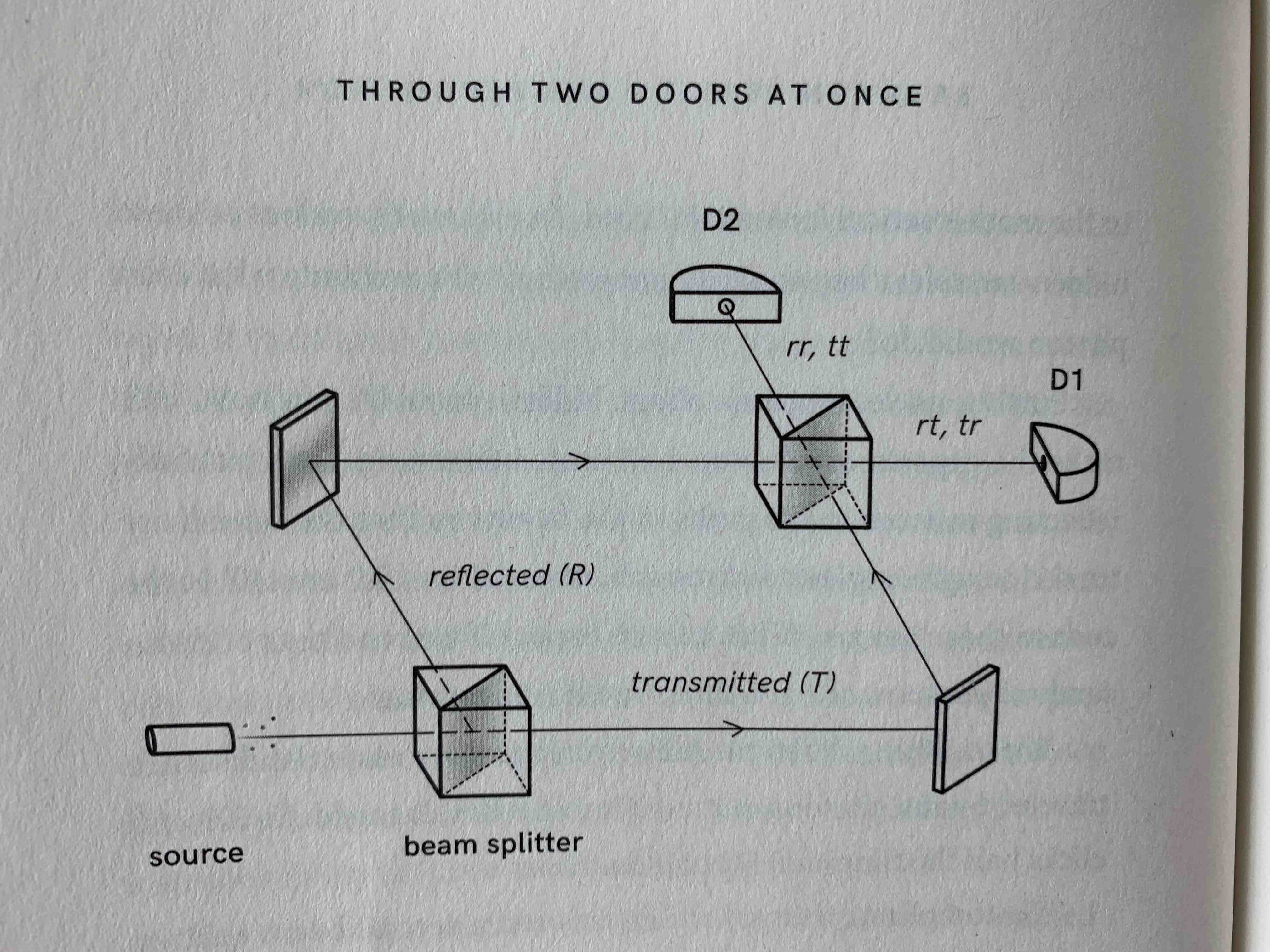
- send 10,000 photons from source
- D1 clicks 10,000 times, and D2 never clicks
Why does interference happen?
- the width of the beam splitter is carefully calibrated such that if a photon is reflected (r) by it, the extra distance it travels is \(\frac{1}{4}\) of a wavelength.
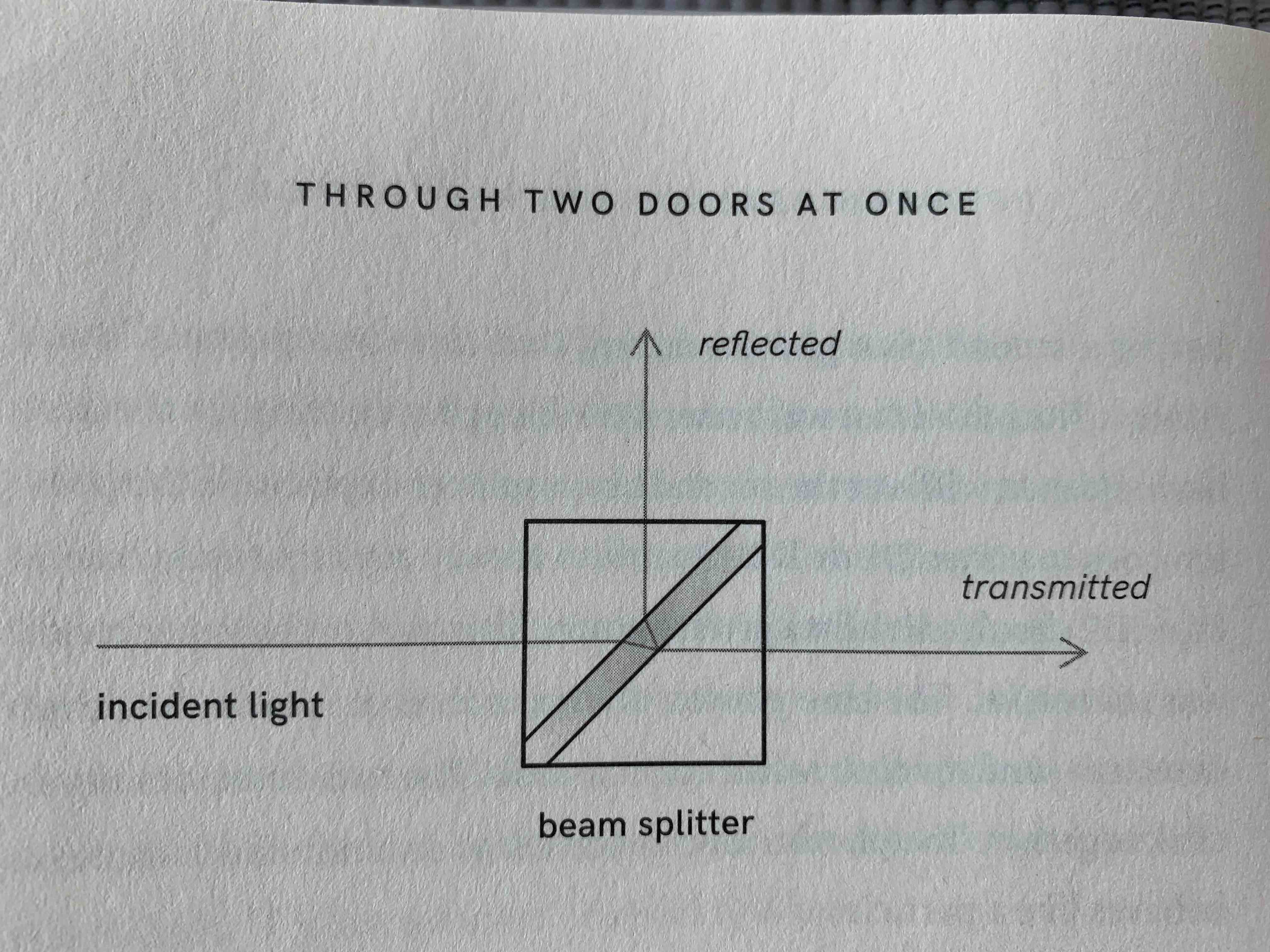
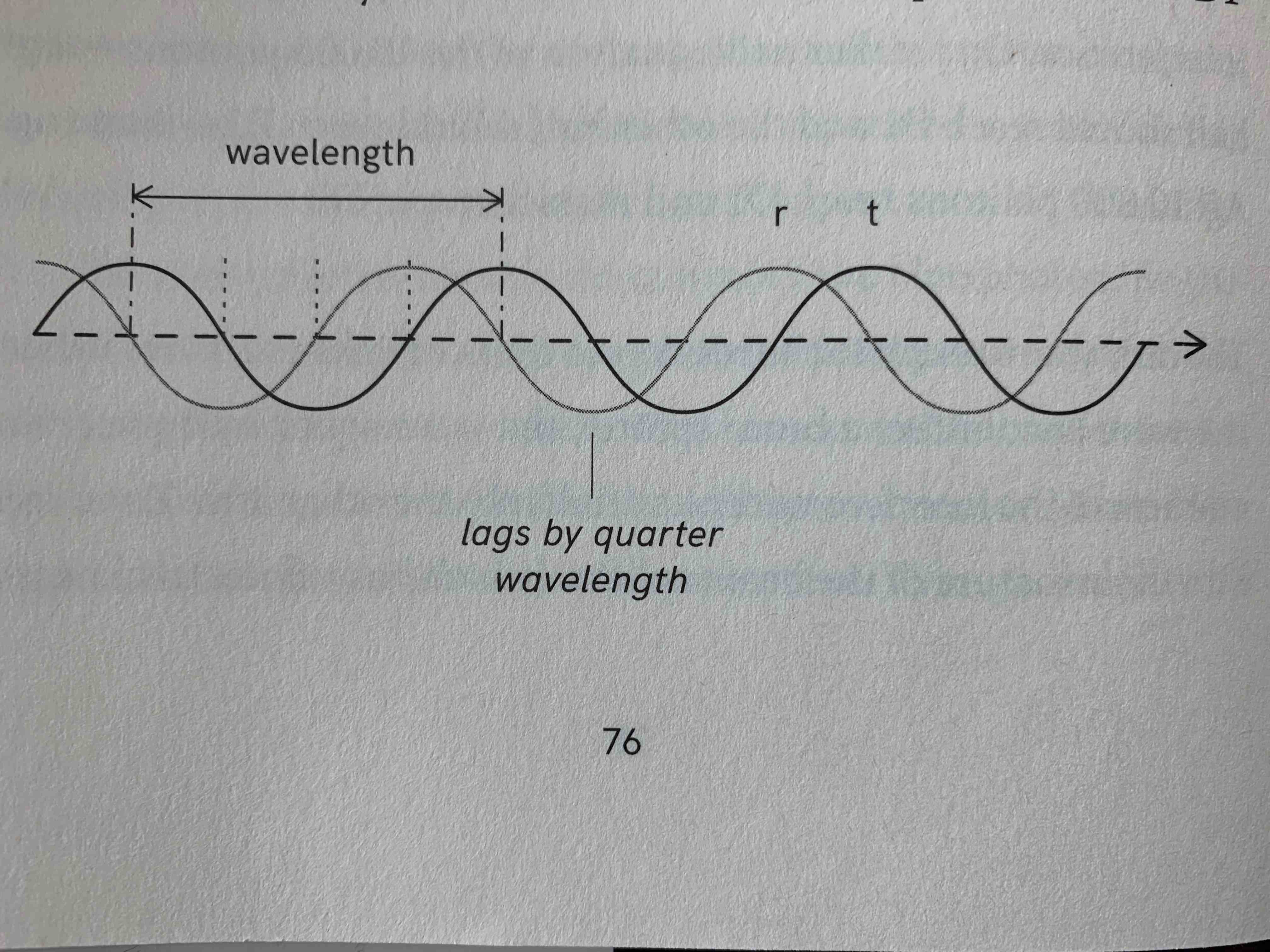
- And if it’s reflected twice (rr), it will travel an extra \(\frac{1}{2}\) of a wavelength more than a photon that was never reflected (tt, i.e. transmitted twice).
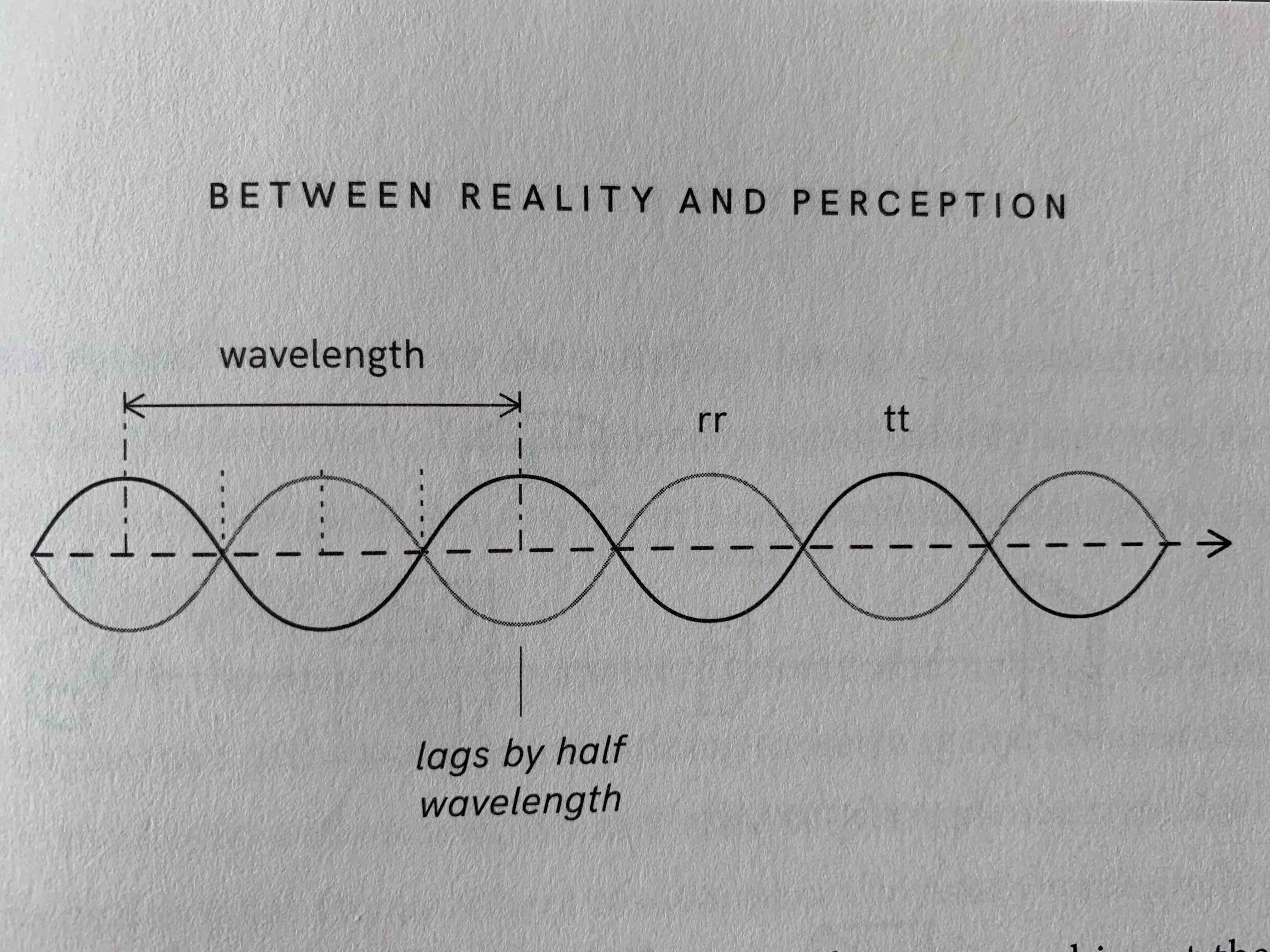
- If you let these two possiblities (rr, tt) interfere with each other, they are perfectly out of phase resulting in complete destructive interference.
#3 Double Slit Experiment 2: 2 beam splitters with block
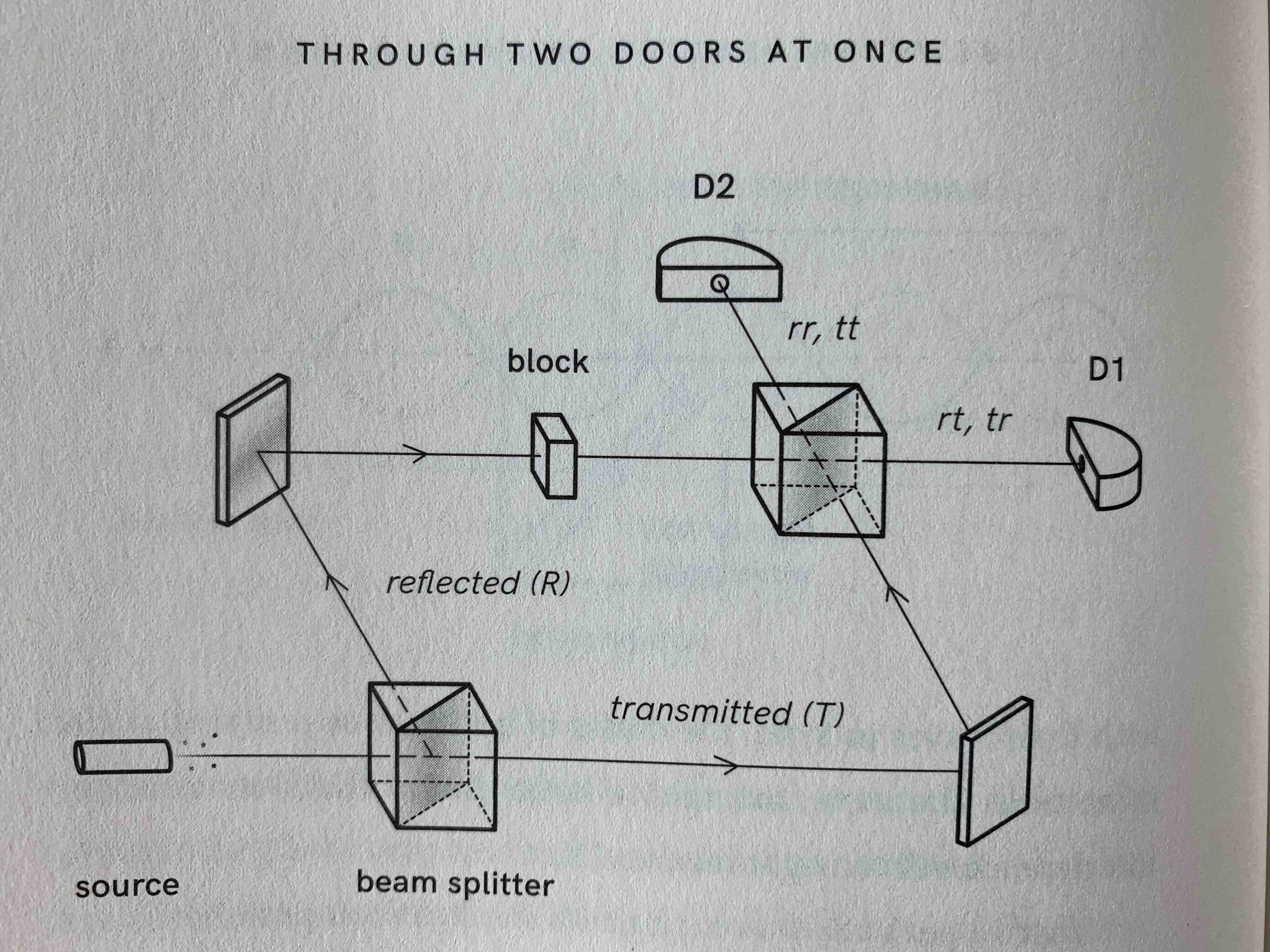
- send 10,000 photons from source
- 5,000 run into block
- D1 clicks 2,500 times
- D2 clicks 2,500 times
Just to reiterate. All we’ve changed from the previous experiment (in which D2 never clicked) is that we’ve eliminated some of the phones by placing a block in their path. And that somehow made the number of photons that hit D2 go from 0 to 2,500… wat.
#4 Delayed Choice Experiment
Wheeler’s thought experiment: What if we delay the choice of whether or not to put in place the second beam splitter until after the photon has gone past the first beam splitter?
At the moment it encounters the first beam splitter, let’s say there is no second beam splitter. From all we know thus far, the photon should go through either one arm or the other, as a particle. After the photon is on its way to either D1 or D2, we insert the second beam splitter and make the two paths look indistinguishable.
What’s the photon to do? Suddenly decide that it has to go into a superposition of taking both paths and display interference with itself?
You can also do the opposite: let the photon enter the interferometer with the second beam splitter in place and then remove it.
2005: What they (Aspect) observed was that there was no fooling the photon. If the second beam splitter was not there, it behaved like a particle, otherwise it acted like a wave. It did not matter when the second beam splitter was inserted.
#5 Bell’s inequality
Need to understand this one better. p. 100-108
#6 Delayed Choice Quantum Eraser Experiment
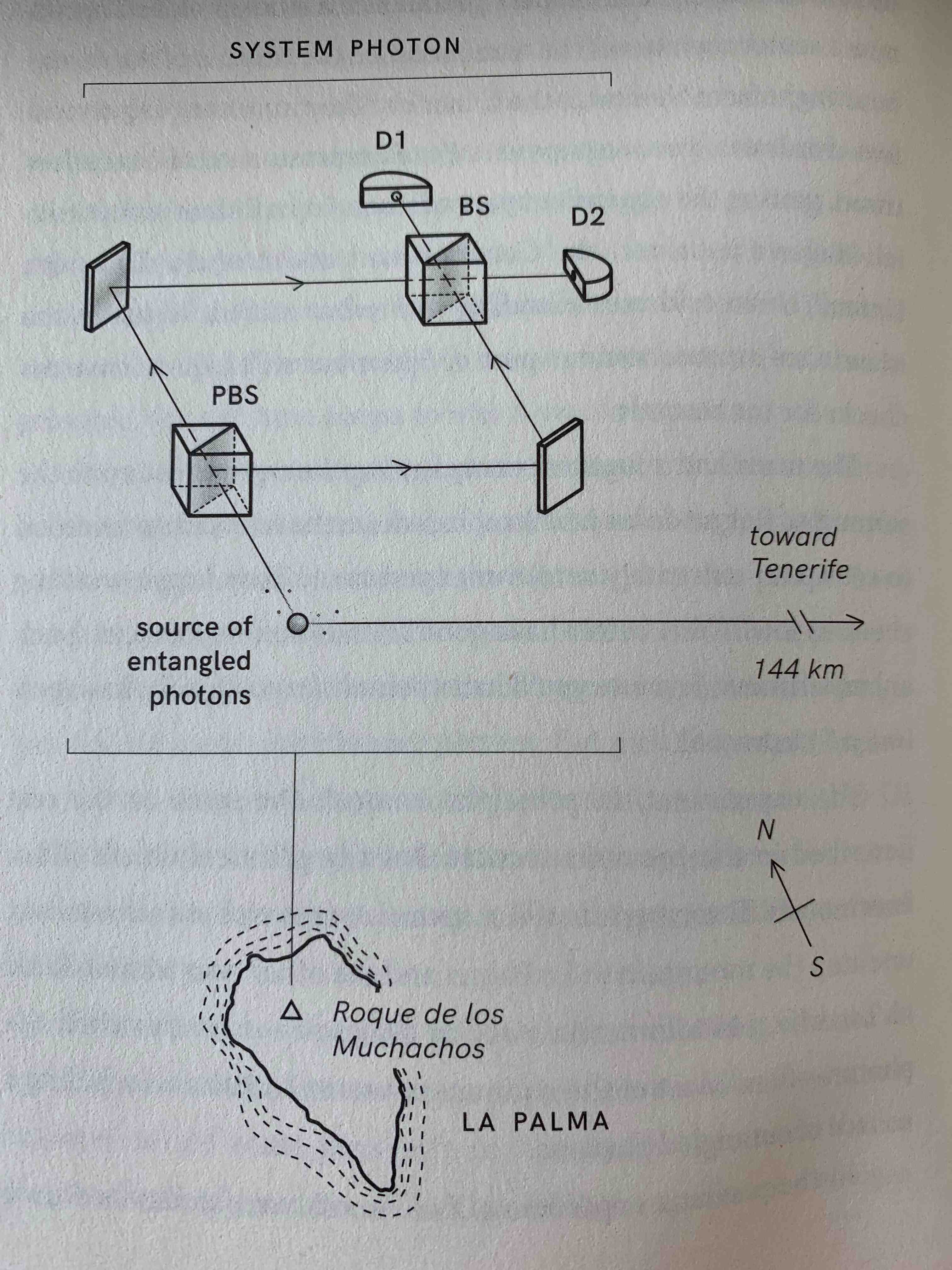
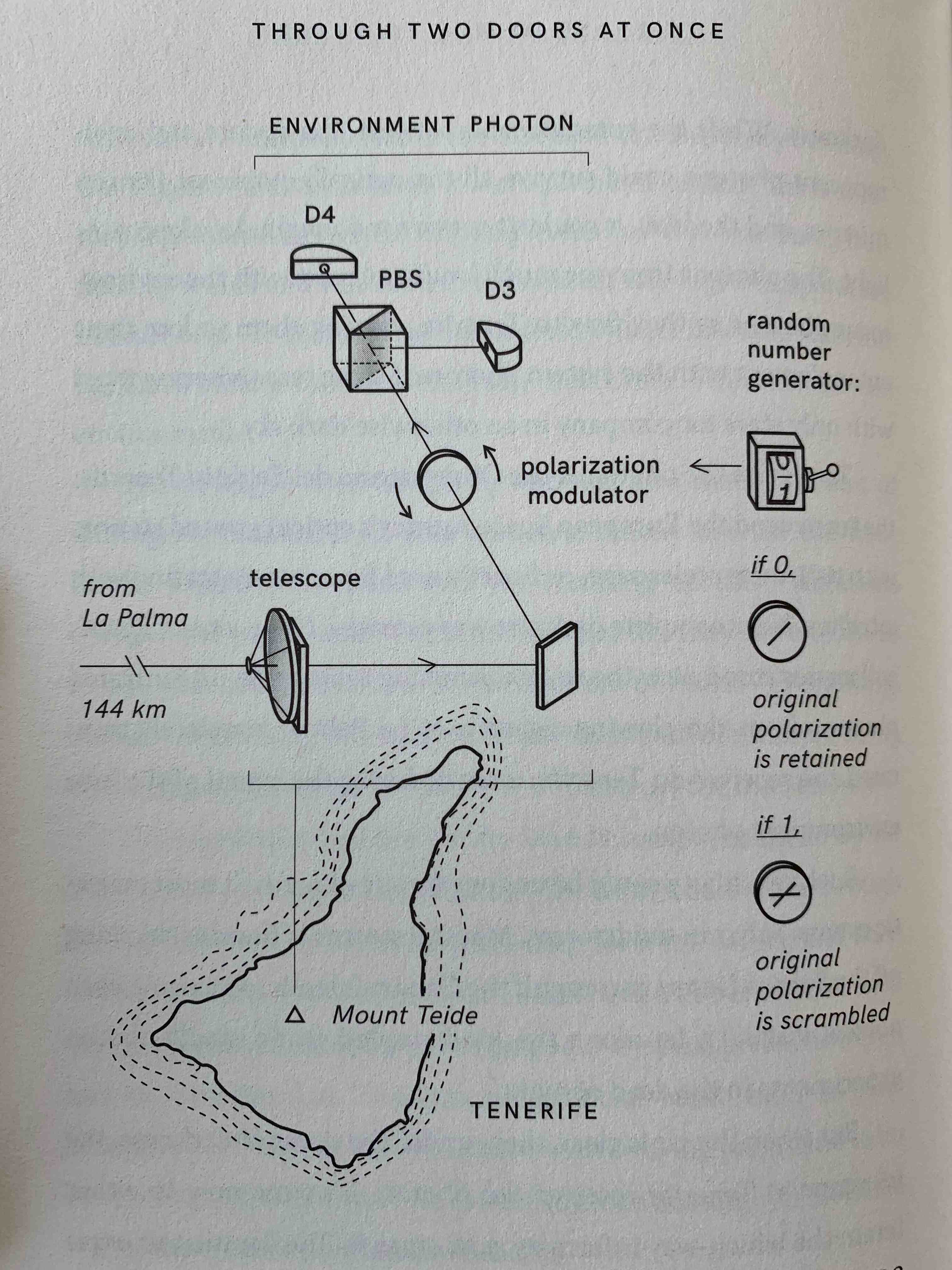
p. 122 & 126 (left and right picture, respectively)
Long quote from p. 125-128:
But when the air is clear, then, under the cover of darkness, the telescope at Tenerife receives the photon. It’s time now to either retain the which-way information or erase it. The decision to erase or not to erase is based on the output of a quantum random number generator.
If it outputs a “0,” the environment photon’s polarizatioin is left untouched and the photon preserves the which-way information about its corresponding system photon as La Palma. The photon then passes through a polarizing beam splitter and ends up at D3 if horizontally polarized, and D4 if vertically polarized. Because of entanglement, we know that the corresponding system photon woudl have been oppositely polarized and thus we know which path it took at La Palma.
But if the random number generator output a “1,” the environment photon’s polarization is scrambled, and the which-way information encoded in the environment photon is erased. It has now a 50 percent chance of going to D3 and a 50 percent chance of going to D4. There’s no way to tell whether the environment photon was horizontally or vertically polarized and so there’s no way to tell which path the corresponding system photon took at La Palma.
The utterly confounding aspect of this experiment is that the measurements at Tenerife - erasing the which-way inforamtion or otherwise - are done some 0.5 milliseconds (an etermity for light) after the system photon has gone through the Mach-Zehnder interferometer and hit either detector D1 or D2 at La Palma. The events at Tenerife and La Palma, according to special relativity, should have no causal influence on each other. Quantum mechanics begs to differ - if one is relying on traditional notions of space and time.
We are now coming to the heart of this experiment. This intricate version of the double-slit experiment combines all the mysterious aspects of quantum mechanics: randomness, wave-particle duality, adn even entanglement.
For those environment photons that were left untouched, if you look now at the clicks made at D1 or D2 by the corresponding subset of system photons at La Palma, you’ll find that there was no interference; they acted like particles: half of them would have gone to D1 and half to D2 when the two arms of the interferometer were of equal length.
But for those environment photons whose which-way information was erased once the environment photons were detected at Tenerife, the corresponding system photons at La Palma showed wavelike behavior: all those photons ended up at D1 and none at D2.
Questions, Continuation Thought Experiments
#1
If a system photon hits D2, then we know that quantum random number generator will output 0 and preserve the polarization (since when it output 1 and the polarization is scrambled, interference occurs s.t. no photons hit D2). What!? So, we can predict a “random” event in the future?
Let’s tweak the experimental setup slightly as a thought experiment. First off, let’s say that 1,000 system/environment photon pairs are all fired off within a period of time less than the time it takes for the first environment photon to get to Tenerife (so, within 0.5 ms). Next, let’s say that instead of the quantum random number generator making a new decision for each environmental photon, it only outputs one number which is then used to decide whether or not the polarization modulator scrambles the polariation for all 1,000 environmental photons. Now, if we’re measuring the clicks at D1 and D2 in La Palma before the quantum random number generator makes its decision, we will see one of two things. Either about 5,000 clicks at D1 and 5,000 clicks at D2, or 1,000 clicks at D1 and none at D2. These outcomes should be quite easy to distinguish from one another. If we see the first outcome (about 5,000 clicks at both detectors), then we know that the quantum number generator will output a 0. If we see the second outcome (10,000 clicks at D1, 0 at D2) then we know it will output a 1. What!?
Let’s make this even more absurd. Let’s say that in Tenerife, they put a man in a booth and tell him to clap his hands every so often. They construct the following contraption based on the claps within the booth. If there was a clap within the last 0.25ms, then the polarization modulator will retain the original polarization (similar to if the quantum random number generator output a 0 in the real experiment). Otherwise, it will scramble the polarization. Then, we repeat the experiment above (the version where we send 10,000 photons in a short amount of time). If we see ~5,000 clicks at both detectors, then we know that he will clap some time between now and the time the photons reach Tenerife. If we see 10,000 clicks at D1 and 0 at D2, we know he won’t clap. What!?
#2
Question about the following quote from p. 128 “this seems to imply superluminal or faster-than-light signaling”. If the decision as to whether or not to scramble the polarization in Tenerife was done before the system photon was measured in La Palma, but before by less than the time it takes light to travel from Tenerife to La Palma, then I would understand that statement. But it happens after! Maybe a more rigorous way to phrase my confusion (since before/after is confusing) is: Regardless of the speed of light, the events in Tenerife would happen after the events in La Palma from the perspective of an observer in La Palma. Right?