The Monty Hall problem is a famously counterintuitive math problem that sparked a heated debate among mathematicians around the country. Here’s wikipedia’s formuation:

Suppose you’re on a game show, and you’re given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what’s behind the doors, opens another door, say No. 3, which has a goat. He then says to you, “Do you want to pick door No. 2?” Is it to your advantage to switch your choice?

If you haven’t encountered this problem before, I highly recommending taking a minute to come up with an answer yourself before continuing.

Warning: spoilers below…

There are two common answers:

  • The first (and incorrect) answer is that it doesn’t matter. There are two closed doors, and they’re both equally likely to have the car behind them.
  • The second (and correct) answer is that the door you initially chose only has a \(\frac{1}{3}\) chance of having the car, and therefore the other closed door has a \(\frac{2}{3}\) chance of having the car. So, you should switch.

Here’s a picture, courtesy of wikipedia:

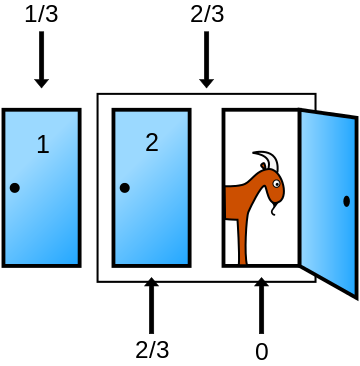
There are many ways to come to terms with the answer, but here is the most intuitive way that I’ve thought to explain it.

Imagine that instead of 3 doors, there are 1,000,002 doors. Behind one door is a car; behind the others, goats. You pick a door, and the host, who knows what’s behind the doors, picks 1,000,000 other doors to open that all have goats behind them. Importantly, he would never open the door with the prize, since that would ruin the game. So, to reiterate, there are

  • 1 million open doors, all of which show goats
  • the closed door that you initially picked
  • and the closed door that the host didn’t open.

Here’s another picture, courtesy of wikipedia (except with a total of 10 doors instead of 1,000,0002):


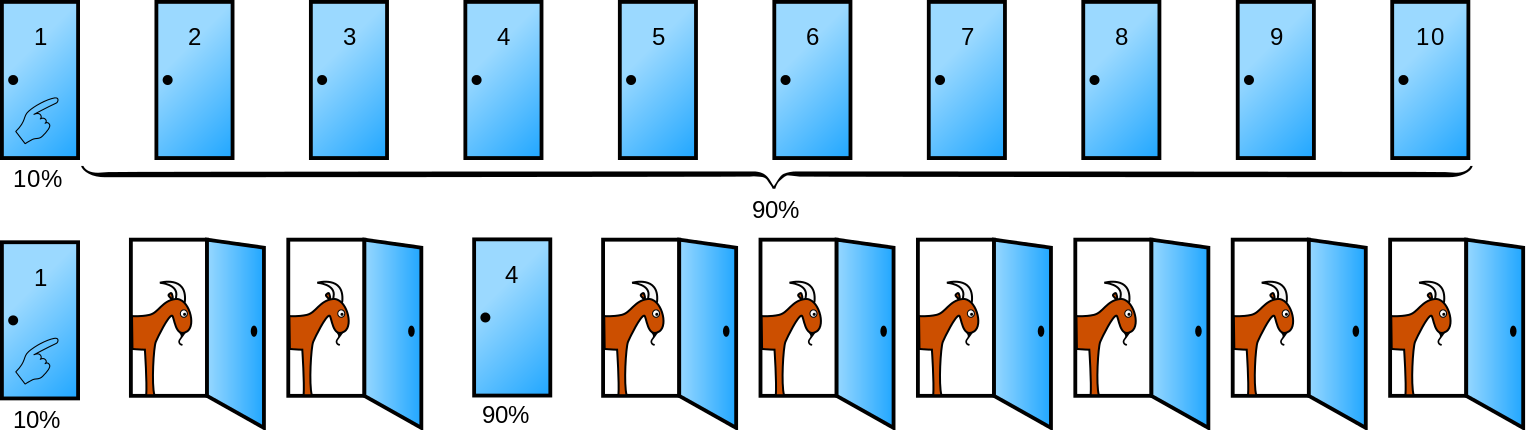
Now, there are two possibilities, either you initially picked the door with the car behind it, and the other closed door has a goat, or you didn’t, and the other door has a car. Which seems more likely?

Obviously, there’s a much bigger chance that you didn’t initially pick the one door (out of 1,000,002) with the car behind it. By increasing the number of doors to such a large number, it seems implausible that somehow both doors would be equally likely to have the car behind them, even though - like the original problem - there are only two remaining closed doors at this point.

Hopefully that helps explain why, in the 3 door case, it’s still more likely that the door that you didn’t pick has the car.