Subtracting times
In my 7 year old’s math class, they’re learning about time. In particular, they’re learning how to figure out how many hours and minutes are between two times.
For example: If it’s 1:45, how long until it’s 5:18?
They way they are taught is by counting up by hours until you get within one hour, and then count up by minutes. Something like this:
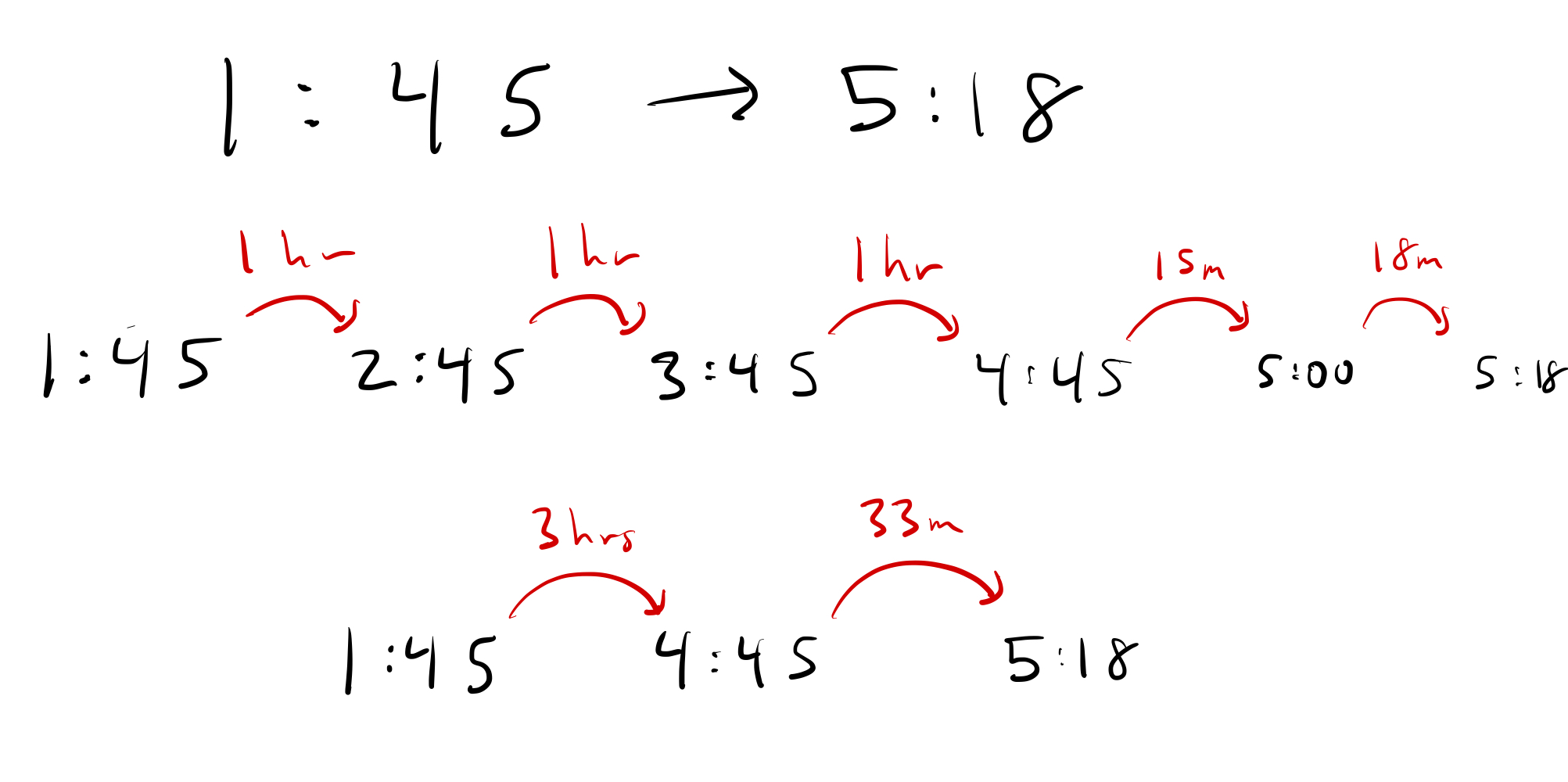
This seems like a totally great way to explain it. Very intuitive.
But I overheard someone say “We do it this way because you can’t just subtract times” and it got me thinking… can’t you?
Like, consider the following “subtraction” problem:
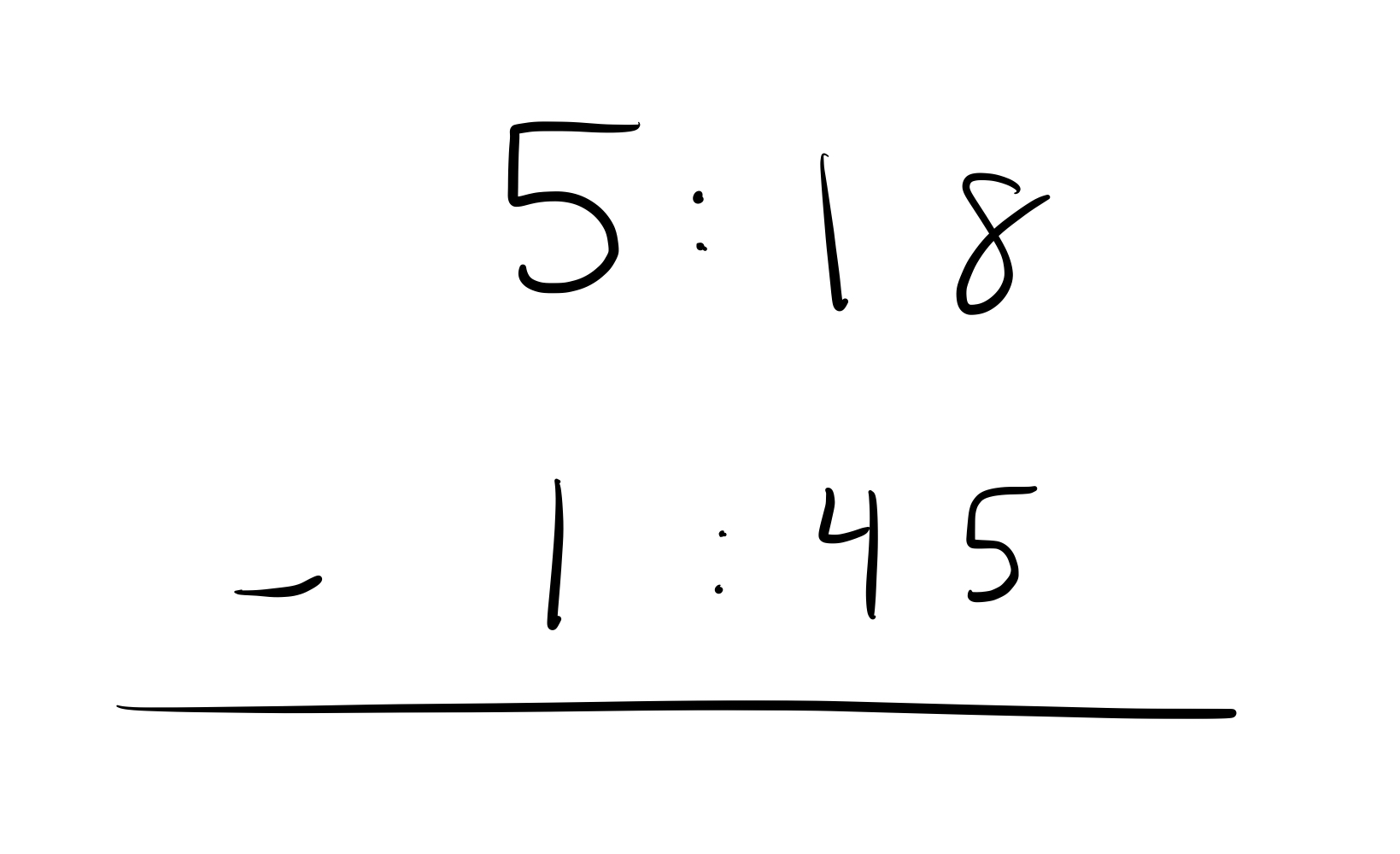
Why can’t we just subtract like usual?
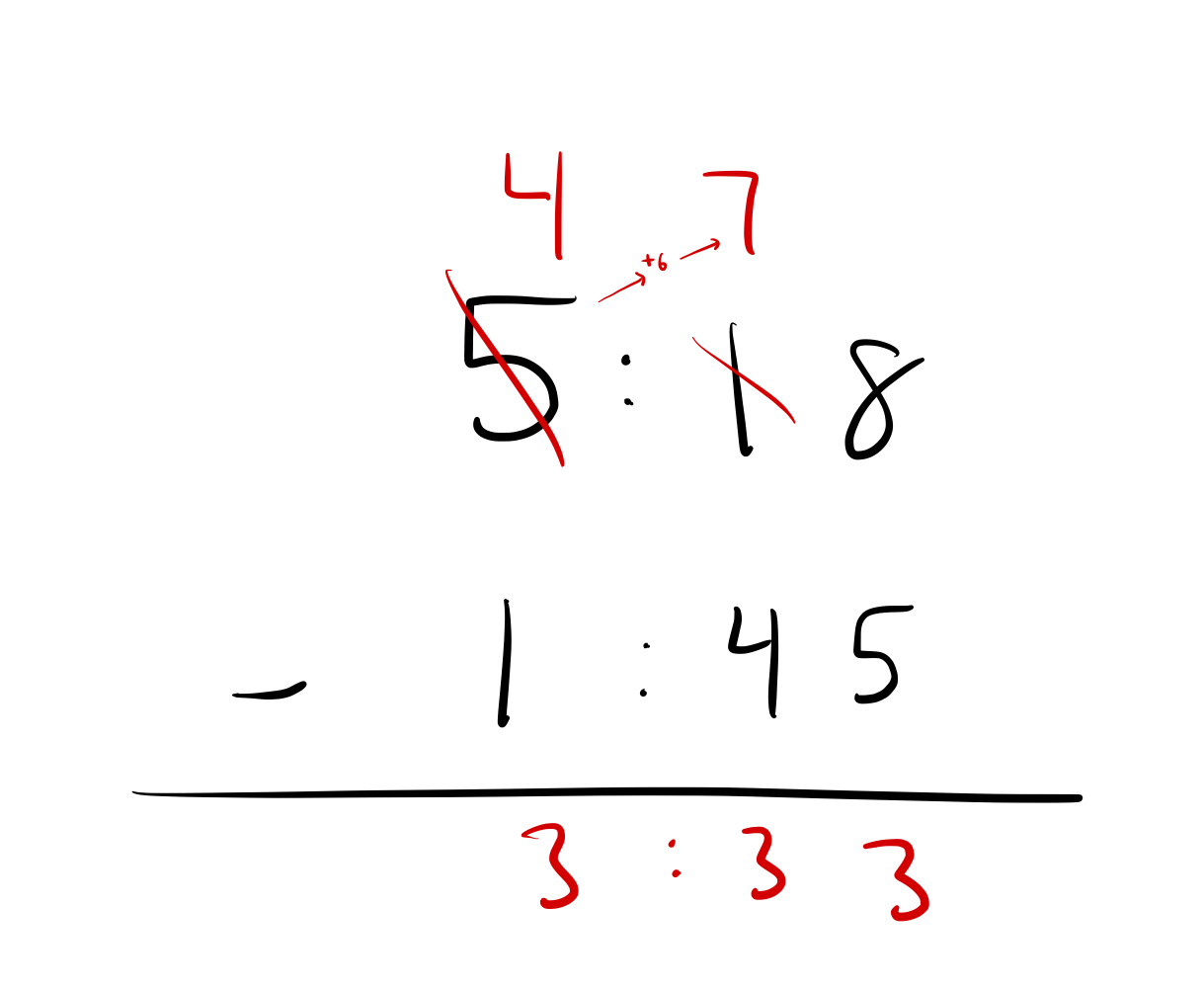
The key is that when you “borrow an hour”, it turns into 6 “10-minutes”, not 10 like we’re used to. From a practical perspective, I totally get why the math class isn’t teaching it this way. It’s a little unusual.
But it makes me a sad because it feels like a fantastic opportunity to give the kids a deeper understanding of what’s really happening when they do subtraction. I worry that kids just accept that when you borrow 1, you get to add 10 to the number to the right – without really getting why.
In order to understand why something in math works the way it does, it’s helpful to try to use it in a foreign situation. Often, these “foreign situations” feel extremely contrived and impractical. But here we have a totally organic situation that allows us to generalize subtraction. And, to be honest, I think subtracting times this way is just plain easier.
Ok, enough soap boxing. This example of subtracting times got me thinking: how far can we push it?
Subtracting more stuff
Let’s try to figure out how much time is between 11:55pm April 9, 2024 and 9:10am Jan 1, 2025:
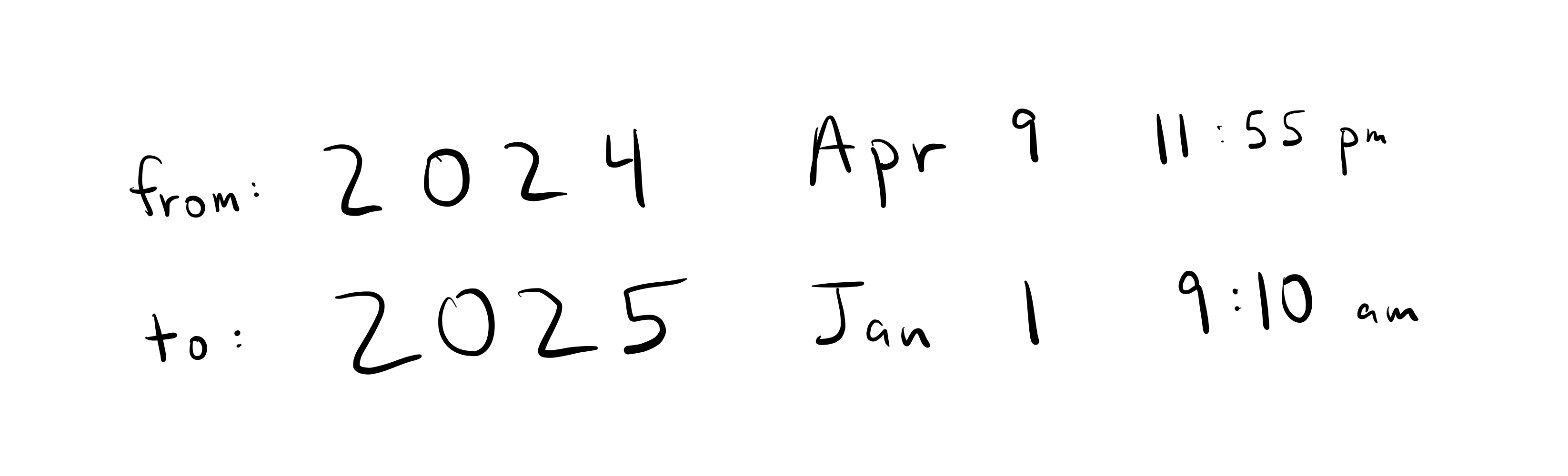
To start, let’s rewrite it as a subtraction problem (doing a little translation in the process):
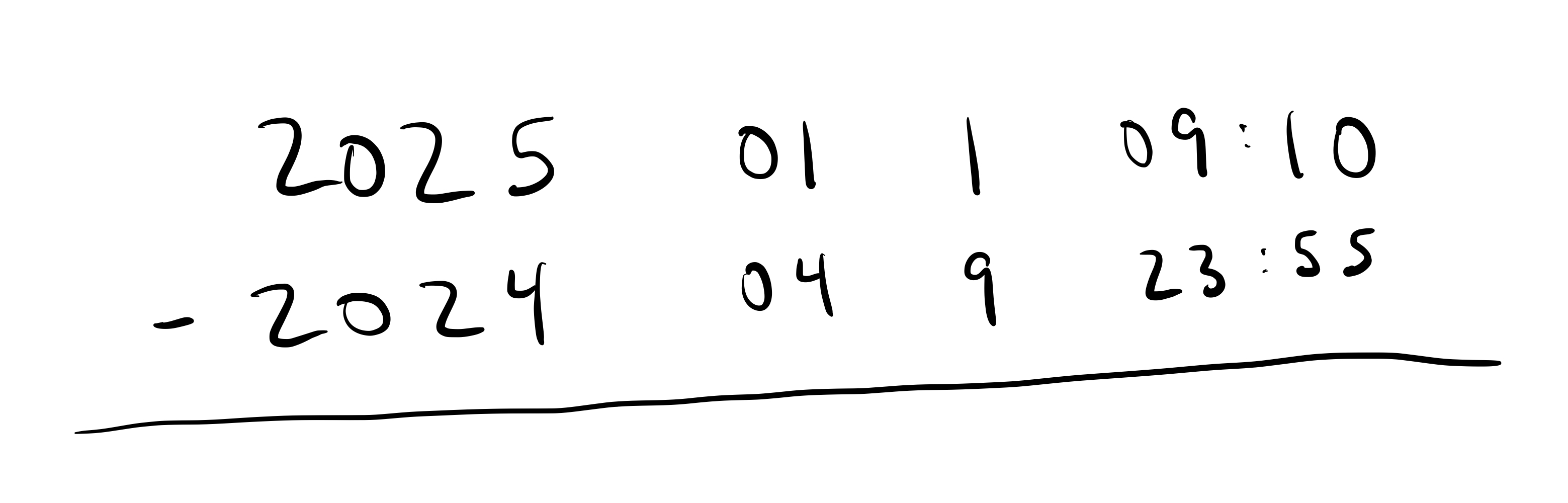
We can proceed to do our subtraction as usual. We already know how to subtract times. We run into our first hiccup when we try to “borrow 1 day”. The problem we run into is that the place value directly to the right of “1 day” is “10 hours”. And you can’t break up 1 day into some integer number of “10 hours” (1 day = 2.4 “10 hours”).
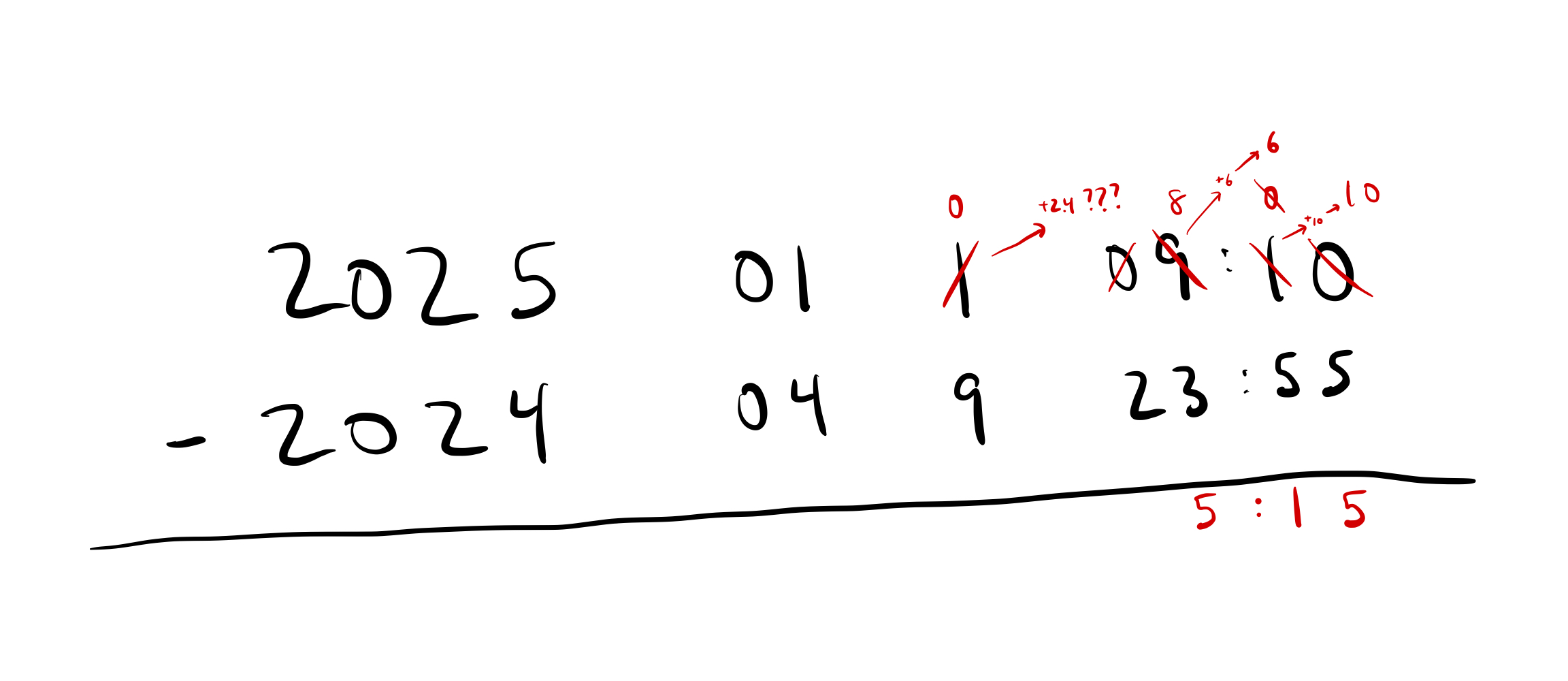
So, we need to modify our algorithm just a bit: instead of subtracting the 8 hours from the 3 hours and then borrowing 1 day, we need to borrow first. Because the borrowing will affect the hours place. Our 1 day turns into 24 hours, and so our “08” hours becomes “32” hours and we can proceed again.
We soon run into another question, when we “borrow 1 month”, how many days does it turn into?
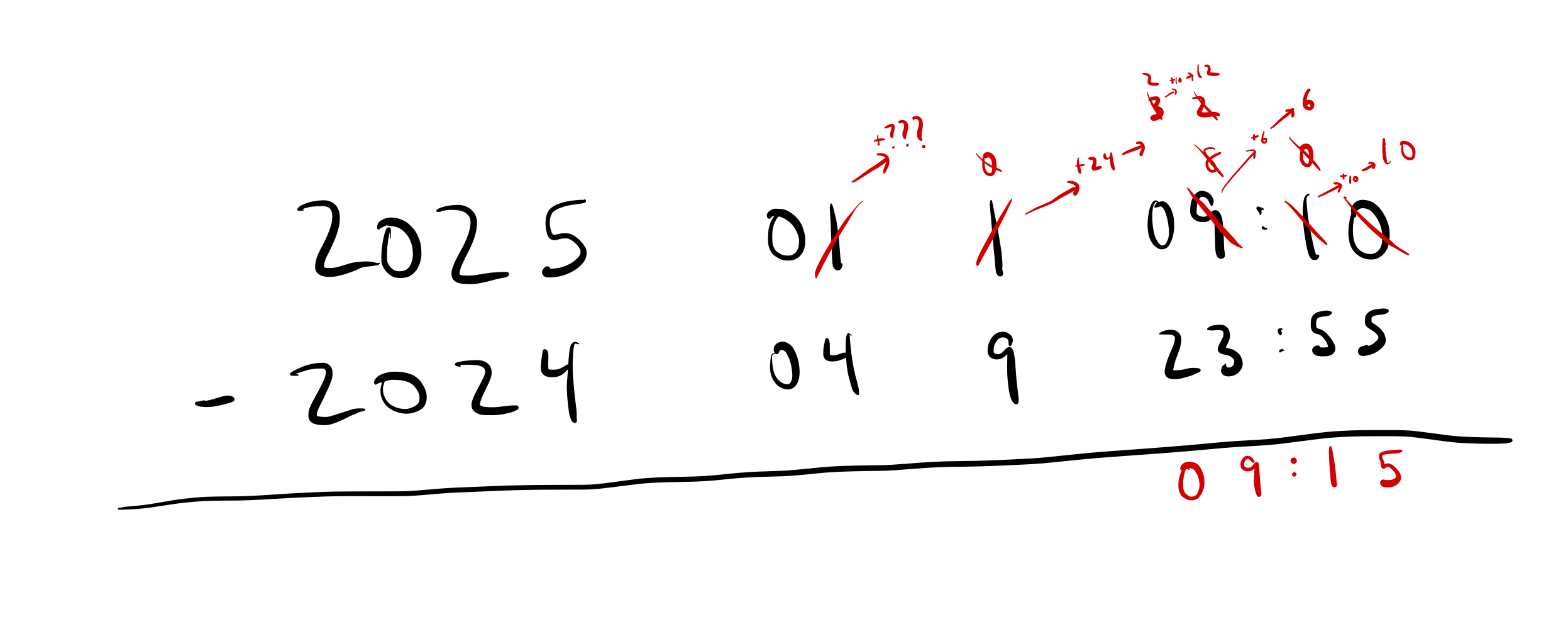
This is a pretty deep question! Let’s take a step back: by subtracting times, we’ve already generalized subtraction to work in scenarios where the conversion ratio between two place values changes depending on which two place values you’re talking about (“10 minutes” = 10 “1 minutes”, but “1 hour” = 6 “10 minutes”).
But here we have a totally new problem: 1 month is not worth a fixed number of days (it depends on the month)! Put another way, we have a non-constant conversion ratio!
When I “borrow January”, how many days should it turn into? You might think 31 since January has 31 days, but for reasons I’ll explain later, I think that’s wrong. I think you should borrow the number of days in Decembers (which, OK, is also 31 but you get the point - it could have been different).
With that out of the way, we can finish our subtration (note: borrowing 1 year has the same problem as borrowing 1 day, it turns into a 12 months which is not an integer number of “10 months”, but we’ve already dealt with this).
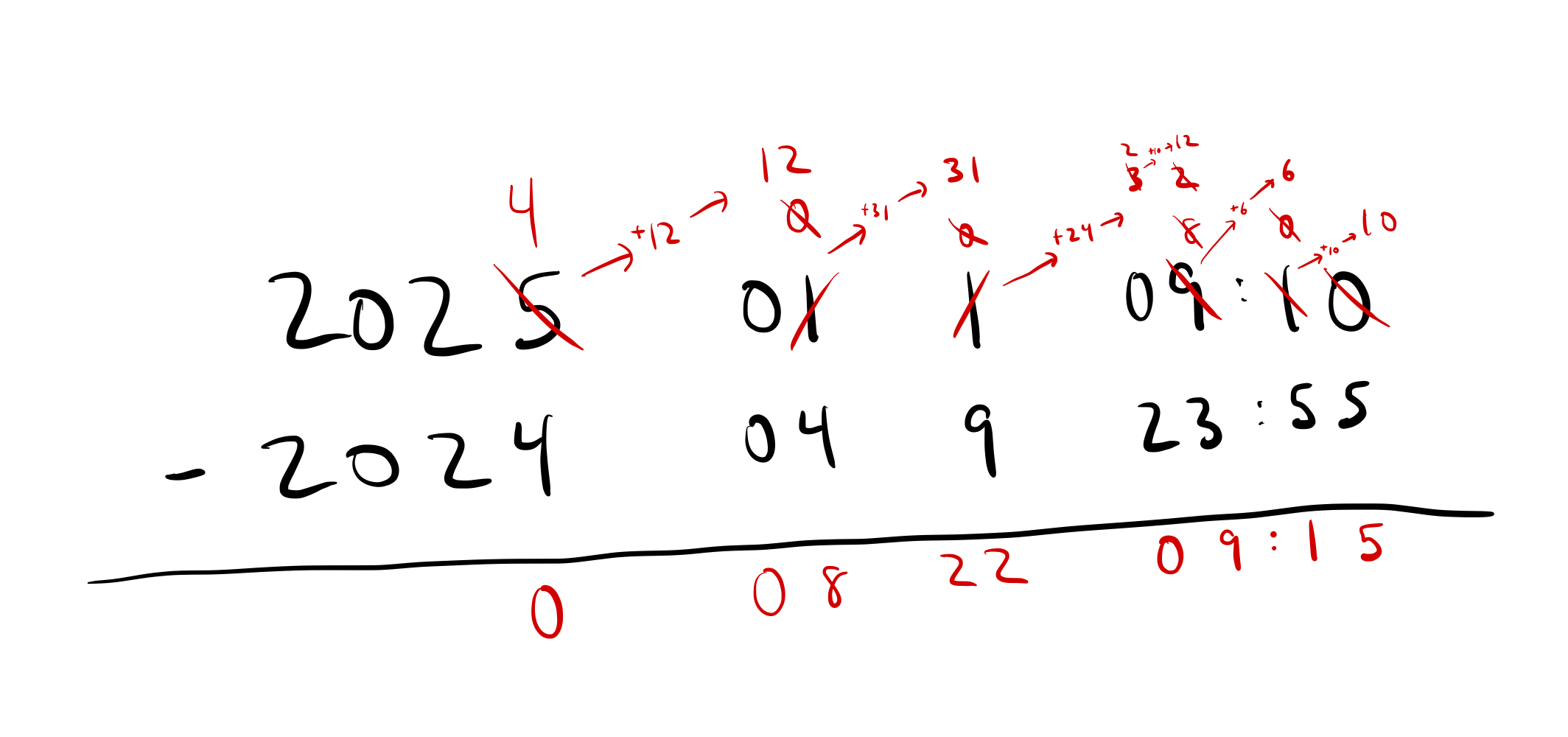
And our answer: 8 months, 22 days, 9 hours, and 15 minutes.
What’s the right way to borrow a month?
I said earlier that when you “borrow January”, you should use the number of days in December. But why? Let’s consider a simpler example: how many days between Feb 27 and Mar 1 (assume it’s not a leap year)?
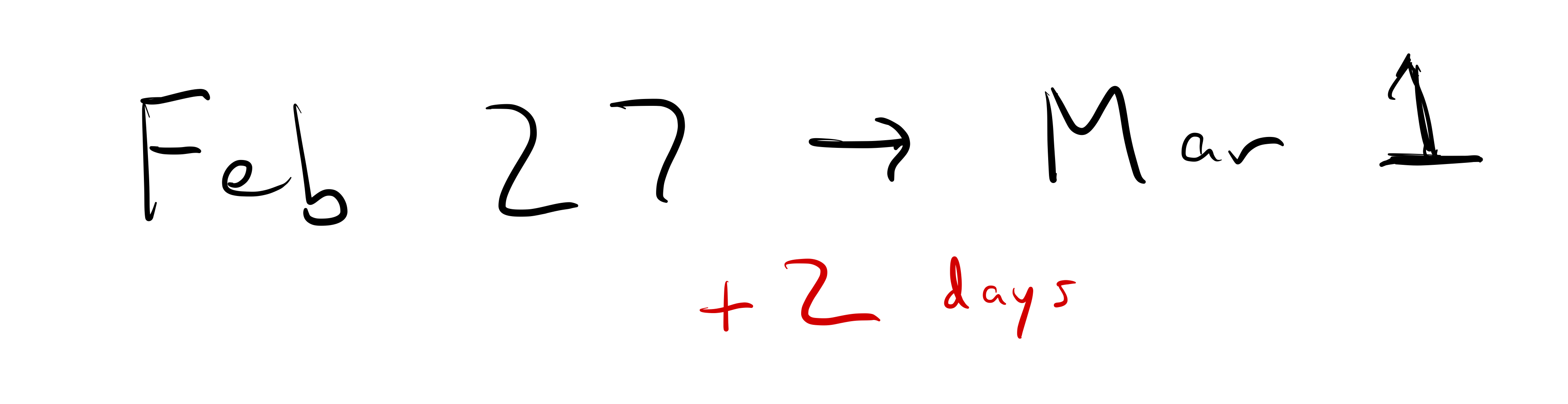
This one is easy enough to do in your head: the answer is unambiguously 2 days. But even though we don’t need to, let’s set it up as a subtraction problem:
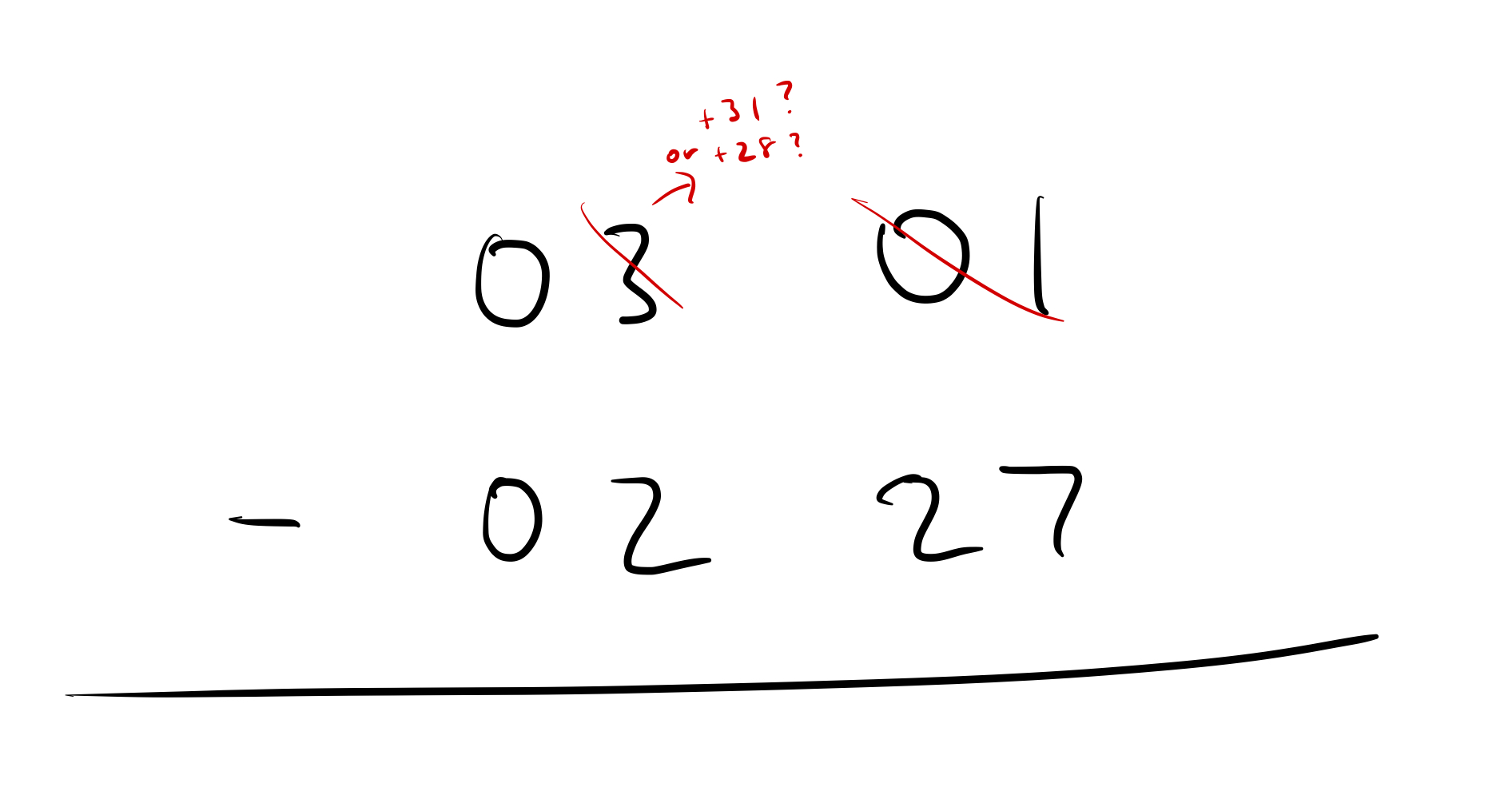
So we need to borrow a month in order to subtract 1 day from 27 days. The question is, when you turn the “3 months” into “2 months”, how many days do you add to the right? Is it:
- 31 days because the 3rd month (Mar) has 31 days?
- or 28 days because the 2nd month (Feb) has 28 days?
Well, we know what the answer is supposed to be, so you can probably guess the right answer: it’s 28 days.
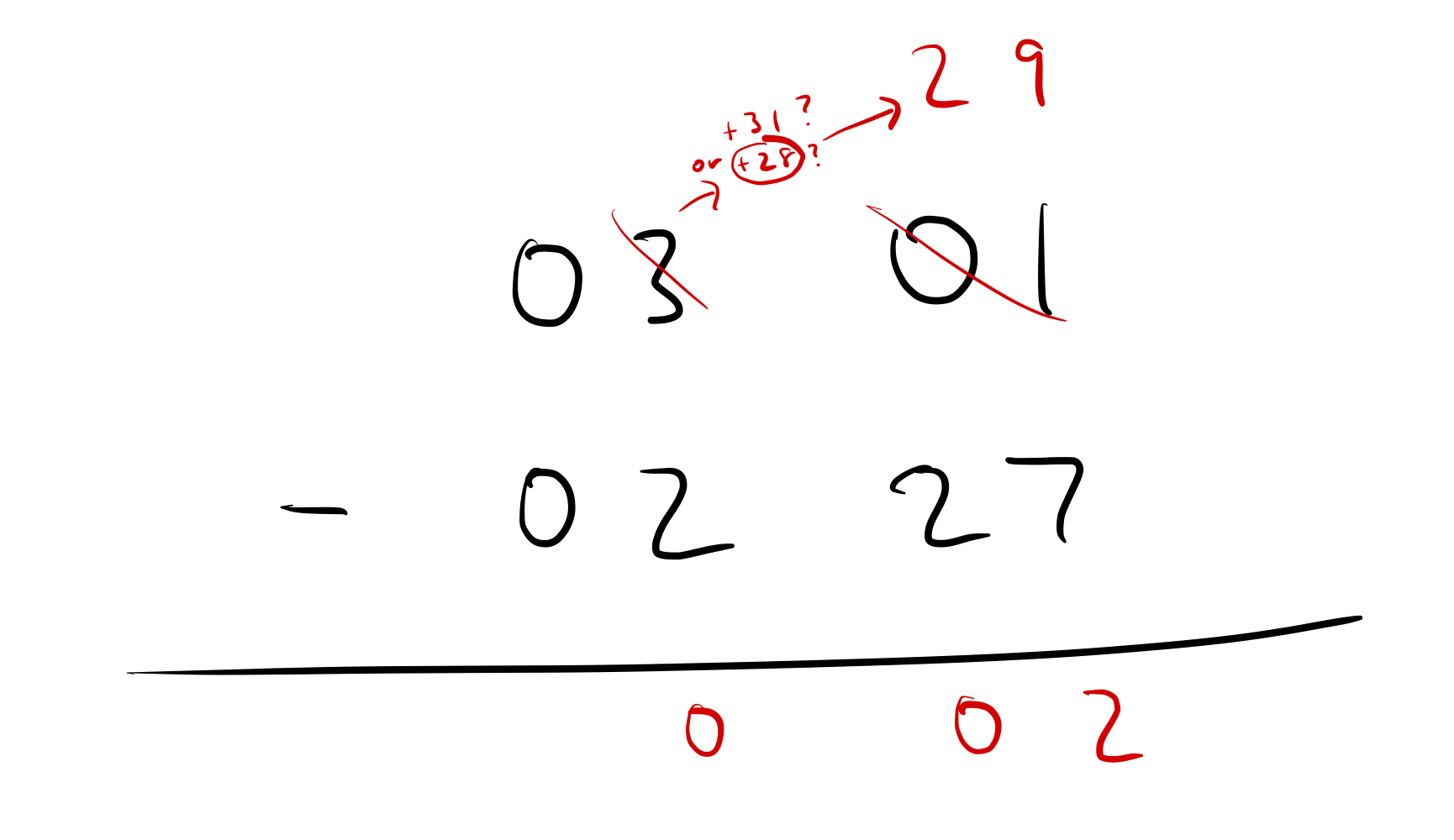
But why is that the right answer?
The way that makes sense to me is that Feb 29 is (in some sense) the same as Mar 1. So that’s why we’re allowed to turn “03 01” to “02 29”. You could argue that’s a circular argument - but it seems clear enough for me.
A quick connection to bases
To some of you, this may be totally obvious, but let me quickly point out the analogy to bases here. Our number system uses base 10, which is why when you borrow, you get to add 10 to the place to the right. An unnecessarily rigorous way to say this is that \(10^{x+1} = 10 * 10^x\).
If we worked in a different base, say 60, then you’d add 60 to the number on the right when you borrowed.
If our number system used different bases for each place value, then you would add a different number depending on which place you were borrowing from. And, well, that’s how time works. Different places use different bases:
- A number \(x\) in the “hours” place is worth \(60x\) minutes
- A number \(x\) in the “days” place is worth \(60\cdot24x\) minutes
- and so on
A problem with non-constant bases
But what about that super weird month place? The number of days a month is worth isn’t even a constant. Is that… even ok?
I think the short answer is no, it’s not. I think having a non-constant base means you can’t really do subtraction anymore. Consider the following question: how many days between Jan 27 and Mar 1?
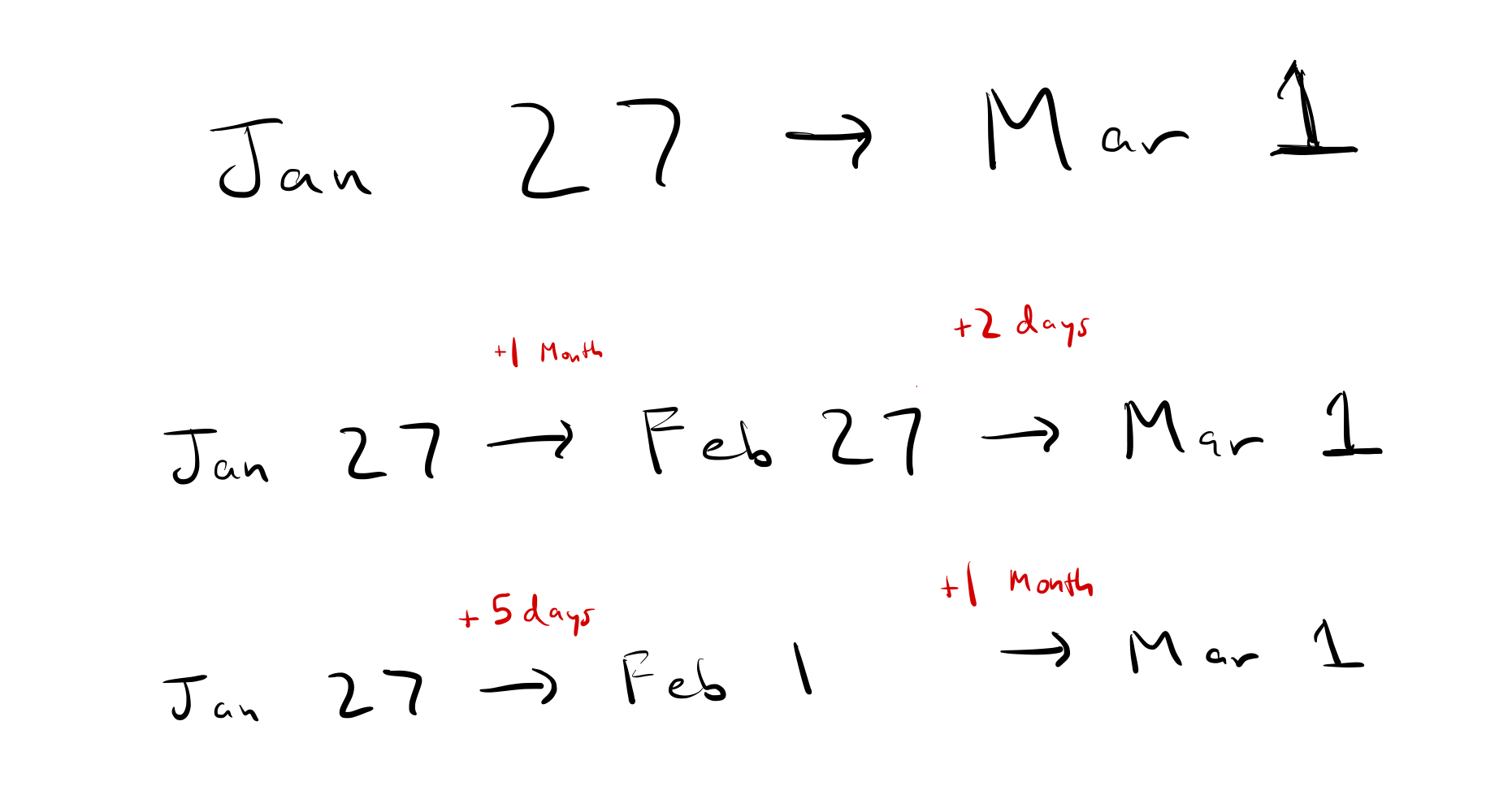
Well, let’s consider two different paths to get there:
- First, we add a month to get to Feb 27, then add 2 days to get to Mar 1.
- But we could also first add 5 days to get to Feb 1, and then add 1 month to get to Mar 1.
This leaves us with two different answers that both feel right:
- 1 month and 2 days
- 1 month and 5 days
If we consider this as a subtraction problem, here are the two ways of solving it:
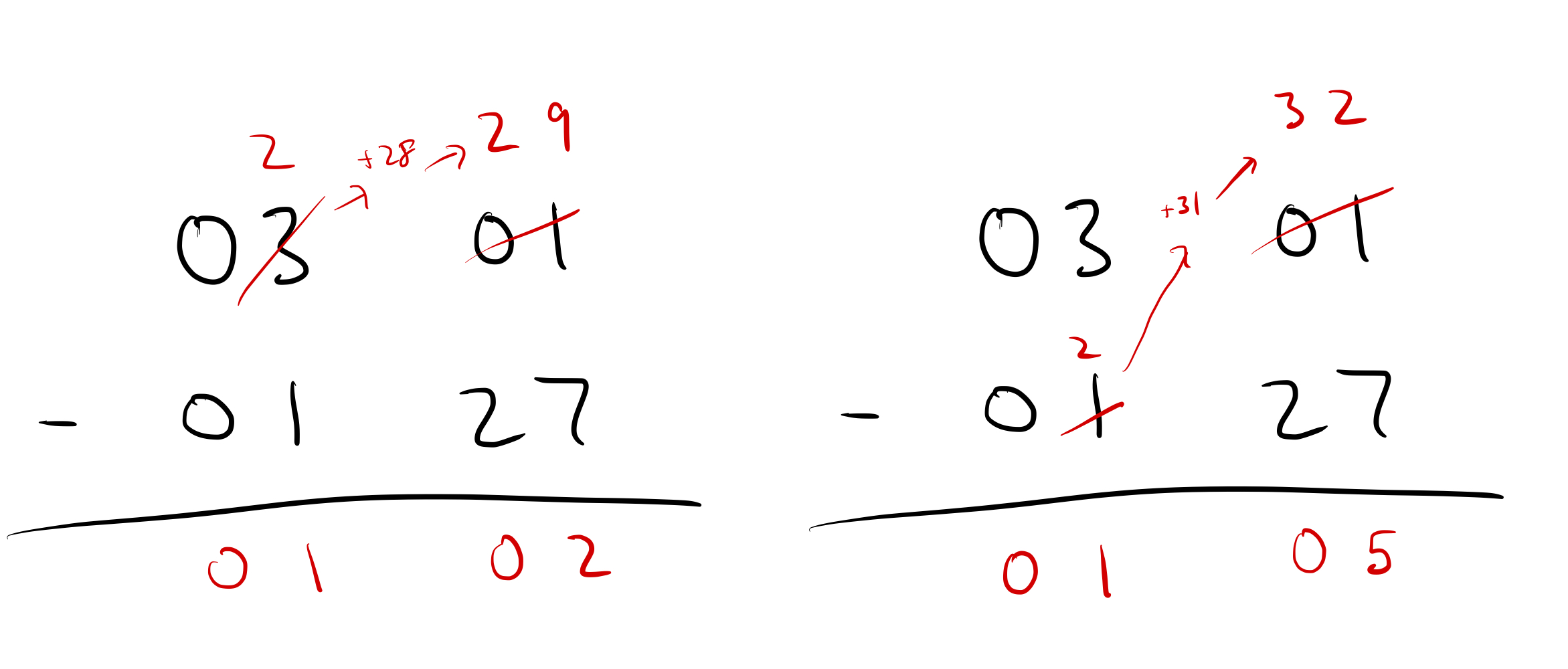
The method on the left should look familiar by now. That’s how we borrowed months before. The method on the right looks… quite weird? I’ve never seen anyone do subtraction by adding 1 to the bottom number (as opposed to subtracting 1 from the top number). But I think it’s valid?
In normal circumstances, subtracting 1 from the top number and adding 1 to the bottom number should have the exact same effect when doing subtraction. But when you have a non-constant base (like months), subtracting from the top number is analogous to counting forward by months, and adding to the bottom number is analogous to counting backwards by months – and they give you different answers.
But why does it fail? I think it fails because if you allow yourself to add both days and months, then your addition becomes non-commutative: the order matters. And so much of math depends on the fact that addition is commutative (and associative). If you break that property, then a lot of things you’re used to doing – like subtraction – become problematic.