Rule of 72

Here’s a handy rule of thumb for calculating compound interest:

If you want to know how many years it will take your money to double, if it grows at a yearly rate of r, just divide 72 by r.

For example, how long would it take for your money to double if it grew at a yearly rate of 5%? $72 / 5 = 14.4$ years. And, sure enough, ${1.05}^{14.4} = 2.01$ !

So let’s say you’re trying to figure out how much money you’ll have saved for retirement if you save now $100, 000 a n d i t g r o w s a t a n a n n u a l r a t e o f 5 y e a r s, s o i n 28.8 y e a r s i t w i l l d o u b l e t w i c e, s o i t w i l l b e a l i t t l e m o r e t h a n$ 400,000. How’d we do? $100, 000 * {1.05}^{30} = 432, 194$ . Pretty good for something you can do in your head!

Probably obvious, but this trick can also convert between a “doubling time” and an interest rate. If I tell you that your money will double in 10 years, you know the interest rate is about $72 / 10 = 7.2 %$ . And, sure enough, ${1.072}^{10} = 2.004$ . Very close!

How does it work?

What’s the equation we’re trying to solve?

(1 + r)^{y} = 2

r is the interest rate
y is the doubling time (the number of years it takes to double)
and 2 is because we want our money to double

We need to turn an exponent into multiplication/division, which usually means taking the log of both sides. Let’s try it:

\begin{aligned} (1 + r)^{y} & = 2 \\ l n ((1 + r)^{y}) & = l n (2) \\ y \cdot l n (1 + r) & = l n (2) \end{aligned}

So far, everything we’ve done is exact. Now it’s time to make a few approximations:

\begin{aligned} l n (2) & \approx 0.693 \\ (for small r) & l n (1 + r) & \approx r \end{aligned}

The first one is trivial, you can just check it with a calculator. Why, though, is the second one true?

You can think about it this way. $e^{0} = 1$ . And the derivative of $e^{x}$ at 0 is also 1. So, if you zoom in really close around 0, it looks like a straight line with a y-intercept of 1 and a slope of 1. Which means, for small values of r, $1 + r \approx e^{r}$ . And if we take the natural log of both sides, we get $l n (1 + r) \approx r$ .

So, using what we have so far, we can say:

\begin{aligned} y \cdot l n (1 + r) & = l n (2) \\ y \cdot r & \approx 0.693 \\ y & \approx \frac{0.693}{r} \end{aligned}

This works just fine, especially for really small values of r. For example, how long would it take for your money to double at a 1% interest rate? 69.3 years right? ${1.01}^{69.3} = 1.99$ . Close!

So where does 72 come from?

Well, $l n (1 + r) \approx r$ gets to be a worse approximation as $r$ gets large. In particular, $r$ is an overestimate for $l n (1 + r)$ .

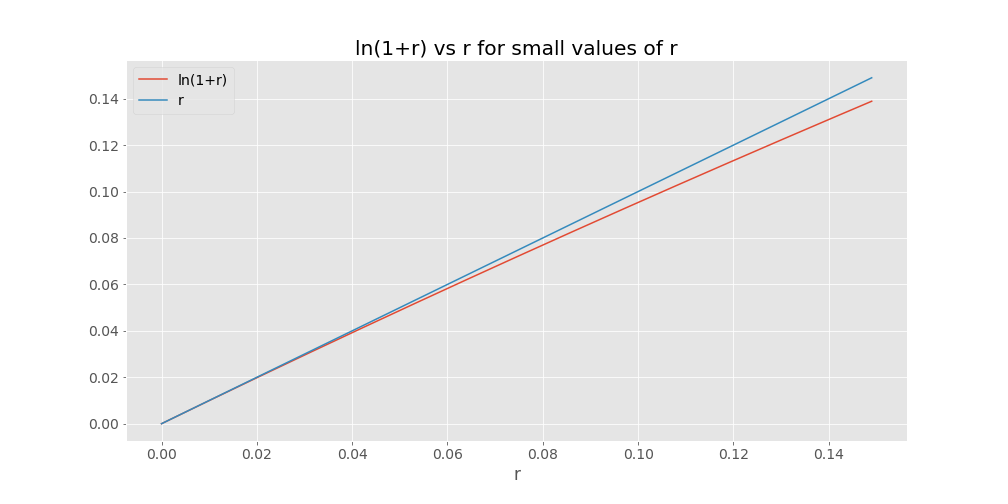
So, when we divide by $r$ in $\frac{0.693}{r}$ , we’re dividing by something that’s too large. For “normal” interest rate values - say, 8% - $r$ is about 4% bigger than $l n (1 + r)$ . So, to adjust for that fact, we can just make numerator 4% bigger as well. What’s $0.693 * 1.04$ ? 0.72!